要旨:java.geomに属するクラスではパラメトリック曲線を扱えないので、このページで説明するクラスを使ってパラメトリック曲線に拡張する。java.geomで提供されている基本図形Rectangle2D,
RoundRectangle2D, Ellipse2D, Line2Dなどがパラメトリック化される図形で、同様な形式のコンストラクターとメソッドを用意する。
パラメトリック曲線は、曲線間の交点計算や点から曲線までの最短距離、最短点を計算するために大層便利である。例えば現在のマウス位置から、画面上に表示されている全ての図形境界までに最短距離を計算し近い図形を選ぶことにより、直線、折れ線、曲線に対して図形の選択を行う(MousePositionLS, SelectionLS)。この計算はマウスが動くたびに実行されるためリアルタイム処理ができるくらい速くなければならない。
|
| このページで説明するクラス:
Segment2D,
Curve2D, Rectangle2DE,
RoundRectangle2DE, Ellipse2DE,
Line2DE, Polyline2DE,
CubicCurve2DE, GeneralCurve2DE,
FergusonCurve2D
|
1. 概要
曲線間の交点計算、点から曲線への最短点計算など、多少便利な図形処理機能を実現するためには、パラメトリック曲線をサポートする必要がある。
パラメトリック曲線とは、曲線の式がパラメータtの関数で定義されており、曲線上の点(x,y)は曲線の式Cx(t), Cy(t)によって次のように表される曲線である(縦ベクトル表示)。
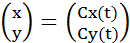 (式1) (式1)
1本のパラメトリック曲線では役に立たないので、パラメトリック曲線を何本か接続して1本の曲線を表す。
例えばjava.awt.geomのRoundRectangle2Dは直線を4本、中心角90°の円弧4本を、直線->円弧->直線->円弧->・・・・と接続する。
 =>
java.awt.geomの機能拡張 =>
java.awt.geomの機能拡張
このとき曲線パラメータは、第1曲線要素は0?t?1の範囲、第2曲線要素は1?t?2の範囲を動くと考える。
例えばRoundRectangle2Dでt=1.5の点は、パラメータの範囲から2番目の曲線要素と分かるので、
(式2)でt=0.5として(x,y)を求める。
以下、接続された曲線もパラメトリック曲線と呼び、個々の曲線要素を曲線セグメント
または単にセグメントと呼び、曲線セグメントの接続点を節点と呼ぶことにする。
またパラメトリック曲線の曲線セグメント数をnumSegとするとき、曲線セグメント番号
を0, 1,..., numSeg-1、節点番号を0, 1,..., numSegと付ける。
曲線セグメントの式
下記の計算式で2次微分まで計算できるようにする。
(1)楕円弧
楕円弧の場合、Arc2Dから取り出せる始角θstartと中心角θextentは度単位。
また画面座標系ではy軸は下向きなので、パラメータtに対して計算するy座標にはマイナスをつける。
なお角度の正方向は反時計周りである。
x=a*cos((θextent*t+θstart)*π/180)+x0(式2)
y=-b*sin((θextent*t+θstart)*π/180)+y0
(x0,y0)は楕円の中心、a,bはx,y方向半径(長半径または短半径)でArc2Dでは次のように取り出す。
a=Arc2D.getWidth()/2, b=Arc2D.getHeight()/2
(2)三次CubicCurve(Bezier曲線セグメント)
P(t)=(1-t)3 Q0 + 3(1-t)2t Q1
+ 3(1-t)t2 Q2 + t3Q3 (太文字はベクトル)
(式3)
表1
|
|
X0(t)
|
X1(t)
|
X2(t)
|
X3(t)
|
|
関数:Xi(t)
|
(1-t)3
|
3(1-t)2t
|
3(1-t)t2
|
t3
|
|
1次微分: Xi'(t)
|
-3(1-t)2
|
3(1-t)(1-3t)
|
3(2-3t)t
|
3t2
|
|
2次微分: Xi''(t)
|
6(1-t)
|
-6(2-3t)
|
6(1-3t)
|
6t
|
表2
|
|
t=0
|
t=1
|
|
関数:P(t)
|
Q0
|
Q3
|
|
1次微分: P'(t)
|
-3Q0+3Q1 |
-3Q2+3Q3
|
|
2次微分: P''(t)
|
6Q0-12Q1+6Q2
=6(Q2-Q1)- 6(Q1-Q0)
|
6Q1-12Q2+6Q3
=6(Q3-Q2)- 6(Q2-Q1)
|
4点で1つの曲線セグメントが作られる。Q0とQ3はセグメントの端点、
Q1とQ2は制御点で一般には通過点ではない。
しばしばQ0~Q3をまとめて制御点と呼ぶ。
一般にスプライン曲線は、複数の曲線セグメントを接続して表す。
この場合、i番目のセグメントの終点とi+番目のセグメントの始点は一致するので一点で表す。
したがってn個のセグメントを接続したスプライン曲線の制御点(通過点を含む)の個数は3n+1である。
(3) Ferguson曲線
Bezier曲線セグメントをつぎのように書き変える。
P(t)= X0(t)Q0 + X1(t)Q1 + X2(t)Q2 + X3(t)Q3
= (X0(t)+X1(t))Q0 + X1(t)(Q1 - Q0 ) - X2(t)(Q3 - Q2 ) + (X2(t)+X3(t))Q3
=(X0(t)+X1(t))P(0) + (X2(t)+X3(t)) P(1) + X1(t)/3 P'(0) - X2(t)/3 P'(1)
=f0(t) P0 + f1(t)P1 + g0(t) T0 - g1(t)T1
最後の式がFerguson曲線セグメント。
ここでP0= P(0), P1= P(1), T0= P'(0), T1= P'(1)
|
|
f0(t)
= X0(t)+ X1(t))
|
f1(t)
= X2(t)+X3(t)
|
g0(t)
= X1(t)/3
|
g1(t)
= X2(t)/3
|
|
関数:fi(t), gi(t)
|
(1-t)2(1+2t)
|
(3-2t)t2
|
(1-t)2t
|
(1-t)t2
|
|
1次微分: fi'(t), gi'(t)
|
-6(1-t)t
|
6(1-t)t
|
(1-t)(1-3t)
|
(2-3t)t
|
|
2次微分: fi''(t), gi''(t)
|
-6+12t
|
6-12t
|
-4+6t
|
2-6t
|
当然、f0(t)= f1(1-t), f0(1-t)= f1(t),
g0(t)= g1(1-t), g0(1-t)= g1(t)の関係式は成立。
一般には複数のFerguson曲線セグメントを接続してスプライン曲線を表す。
この場合、i番節点では手前のセグメントを補間する接ベクトルT1と、
後のセグメントを補間する接ベクトルT0を記憶する。
このT1をTin、T0をToutと表す。
つまりi番節点は、位置P[i]、接ベクトルTin[i]、Tout[i]で表すことができる。
一般に滑らかな曲線に場合、Tin[i]とTout[i]の方向は一致するが、ベクトル長は一致しない。
2. Segment2Dクラス
戻る=>page top
public class Segment2D
Segment2Dは曲線セグメントのクラスである。
このクラスで使う図形データは、java.awt.geomパッケージのLine2D, Arc2D, CubicCurve2Dである。
2 次パラメトリック曲線QuadCurve2D クラスは、あまり使い道がないようなのでサポートしていない。
Segment2Dの主要機能は曲線パラメータt(0?t?1)を与えたときに、曲線上の点の座標、接ベクトル、
接ベクトルの微分ベクトル(2次微分)を計算することである。
計算式は曲線セグメントの式を使う。
|
フィールド
|
説明
|
|
type
|
int type:曲線セグメントの種類を表す。staticな定数LINE, ARC, CUBICのいずれかをセット。
|
| shape |
private Shape shape
typeに応じてjava.awt.geomパッケージのLine2D, Arc2D, CubicCurve2Dオブジェクトのいずれかを設定する。
|
|
affineTransform
|
private AffineTransform affineTransform
特に楕円(弧)を回転した場合など、Arc2Dでは表せなくなるので、このAffineTransformを使用する。
type=LINE, CUBICの場合はデータそのものを変換してしまうので使用しない。
|
|
MOVETO
|
public static final int MOVETO=0
typeにセットする定数。直線を描画せずに移動することを表す。
|
|
LINE
|
public static final int LINE=1
typeにセットする定数。直線であることを表す。
|
|
ARC
|
public static final int ARC=2
typeにセットする定数。円弧であることを表す。
|
|
CUBIC
|
public static final int CUBIC=3
typeにセットする定数。三次Bezier曲線であることを表す。
|
|
QUAD
|
public static final int QUAD=4
typeにセットする定数。2次Bezier曲線であることを表す。
|
|
メソッド
|
説明
|
|
コンストラクタ
|
public Segment2D(int type, Shape shape)
フィールドtype, shape, affineTransformに引数の値をセット。affineTransform=nullを設定。
|
|
コンストラクタ
|
public Segment2D(int type, Shape shape, AffineTransform affineTransform)
フィールドtype, shape, affineTransformに引数の値をセット。
|
|
getType
|
public int getType()
曲線セグメントの種類を問い合わせる。MOVETO, LINE, ARC, CUBIC, QUADのいずれかを返す。
|
| isAffineTransform |
public boolean isAffineTransform()
affineTransform=nullでなければtrueを返す。 |
|
getShape
|
public Shape getShape()
通常はフィールド変数shapeを返す。
shapeがArc2DでaffineTransformがnullでない場合、Arc2DとaffineTransformを設定したGeneralPathオブジェクトを作成して返す。
 =>
getShapeの特別なケース =>
getShapeの特別なケース
|
|
getP
|
public Point2D getP(double t)
引数:
t - 曲線セグメントパラメータ.. 0≤t≤1.
戻り値:
曲線パラメータtに対して曲線上の点を計算して返す。typeに応じた計算式を使う。
|
|
getTangent
|
public Vector2D getTangent(double t)
引数:
t - 曲線セグメントパラメータ.. 0≤t≤1.
戻り値:
曲線パラメータtに対して接線ベクトルを計算して返す。
|
|
getTangentDerivative
|
public Vector2D getTangentDerivative(double t)
引数:
t - 曲線セグメントパラメータ.. 0≤t≤1.
戻り値:
曲線パラメータtに対して接線ベクトルの微分ベクトルを計算して返す。
|
|
getSegmentLength
|
public double getSegmentLength(double t1, double t2)
曲線パラメータt1,t2区間の曲線長を計算する。
折れ線近似で計算するので高精度ではないがDrawProtoでは十分である。
|
|
getBoundingBox
|
public Rectangle2D getBoundingBox()
曲線セグメントを囲むBounding Boxを作成する。
|
|
getBoundingBox
|
public Rectangle2D getBoundingBox(double t1, double t2)
曲線セグメントのt1,t2区間を囲むBounding Boxを作成する。
getTrimmedSegmentで切断されたセグメントを作成してBounding Boxを作成する。
|
|
resizeSegment
|
public Segment2D resizeSegment(Rectangle2D oldBox, Rectangle2D newBox)
引数:
oldBox- ドラッグ開始点と位階前のドラッグ点を対角とする矩形。
newBox- ドラッグ開始点と現在点を対角とする矩形。
戻り値:
リサイズしたSegment2Dオブジェクトを返す。.
処理:
曲線セグメントのリサイズを行う。ARCセグメントでフィールド変数affineTransformがnullでない場合、
リサイズ用の変換マトリックス(Matrix2D.getResizeMatrix)を作成し、
現在のaffineTransformに掛ける。
|
|
trimSegment
|
public Segment2D trimSegment(double t1, double t2)
引数:
t1- 切断開始点パラメータ。.
t2- 切断終了点パラメータ。.
0≤t1, t2≤1
戻り値:
切断されたSegment2Dオブジェクトを返す。
|
|
getFergusonCurve
|
public FergusonCurve2D getFergusonCurve()
曲線セグメントのタイプがLINEまたはCUBICの場合、1セグメントのFergusonCurveを返す。
ARCの場合、楕円弧/円弧を近似する複数セグメントのFergusonCurveを返す。
近似誤差は単位円で1e-8程度であり、中心角では約20度ピッチである。
|
|
transformSegment
|
public Segment2D transformSegment(Matrix2D M)
曲線セグメントにマトリックス変換を施して返す。ARCセグメントの場合、
フィールド変数affineTransformにマトリックスMを掛けた結果をフィールド変数affineTransformに設定する。
|
|
reverseSegment
|
public Segment2D reverseSegment()
曲線セグメントの方向を反転したものを返す。
|
| moveSegmentEndPT |
public Segment2D moveSegmentEndPT(int index, Point2D newPT)
引数:
index- indexが0ならば始点を、1ならば終点を動かす。
newPT- 新しい端点。
戻り値:
始点または終点newPTに動かしたSegment2Dオブジェクトを返す。
処理:
・セグメントの種類がLINEの場合:端点を置き換えるだけ
・セグメントの種類がARCの場合
Matrix2D.getRotationMatrix
で回転と拡大/縮小変換のマトリックスを作成し
this.transformSegmentを呼ぶ。
・セグメントの種類がCUBICの場合
このクラスのgetFergusonCurveでセグメントをFergusonCurveに変換。
FergusonCurve2D.movePointで端点を移動。
FergusonCurve2D.getCubicCurve2DE
でjava.awt.geom.CubicCurde2Dを取得し、shapeフィールドにセットする。 |
| moveSegmentTangent |
public void moveSegmentTangent(int index, Vector2D newTangent)
引数:
index- indexが0ならば始点の接線ベクトルを、1ならば終点の接線ベクトルをnewtangentになるように動かす。
newTangent- 接線ベクトル。
戻り値:
接線方向を変更したSegment2Dオブジェクトを返す。
処理:
このメソッドは曲線セグメントがCUBICの場合だけ有効である。
FergusonCurve に変換し、FergusonCurve.moveSegmentTangentで設定する。
最後はFergusonCurve2D.getCubicCurve2DEでjava.awt.geom.CubicCurde2Dを取得し、
shapeフィールドにセットする。
|
| clone |
public Object clone() 複製を作る
|
|
toString
|
public String toString() 文字列表現を返す
|
|
getSerializableSegment2D
|
public SerializableSegment2D getSerializableSegment2D()
ファイルに書き込むための曲線セグメントのデータを取り出す。
 =>
SerializableSegment2D =>
SerializableSegment2D
|
 :getShapeの特別なケース :getShapeの特別なケース
Shape shape=this.shape;
if(this.type==ARC&&this.affineTransform!=null){
GeneralPath generalpath=new GeneralPath();
generalpath.append(shape, false);
generalpath.transform(this.affineTransform);
shape=generalpath;
}
return shape;
3. The extension of java.awt.geom (geomExtension)
戻る=>page top
java.awt.geomパッケージに含まれるRectangle2D, RoundRectangle2D,………などをパラメトリック曲線として扱えるようにする。
パラメトリック曲線化したクラスはクラス名の末尾に"E"を付けて表す。Rectangle2DE, RoundRectangle2DE,………など。
これらのクラスでは概要で述べた曲線セグメントの式を使って、パラメータtを渡すと、曲線上の点、接ベクトル、2次微分ベクトルなどを計算できる。
またjava.awt.geomパッケージのクラスと同様のコンストラクタが使え、図形の描画、点の内外判定のためにjava.awt.Shapeデータを取り出せるようにする(getShapeメソッド)。
Shapeインタフェースをインプリメントしたクラスは、特に閉図形の場合、指定した点が図形内部にあるか否かを判定するcontainsメソッドを提供してくれるので有益である。
このメソッドはMousePositionLSで多用する。
|
機能
|
実現方法
|
|
パラメトリック曲線機能
|
概要で述べたように曲線セグメント(Segment2D)を並べておけば、
Segment2DのgetP、getTangent、getTangentDerivativeメソッドを使って、
曲線上の点、接ベクトル、接ベクトルの微分ベクトル(2次微分)を計算する。
下の具体例はjava.awt.geom.RoundRectangle2Dパラメトリック曲線化したRoundRectangle2DEである。
コンストラクタはjava.awt.geom.RoundRectangle2Dと同型で、
パラメトリック曲線化のため8個のSegment2Dオブジェクトを作成し、
this.segmentsに設定している。
|
|
java.awt.Shapeデータの作成と取り出し
|
java.awt.geom.GeneralPathはShapeインターフェイスを実装したクラスで、
Line2D, Arc2D, CubicCurve2Dなどを接続した曲線を作成できる。
下の具体例でGeneralPathオブジェクトにgeneralPath.append(shape,true)
で要素を加えている部分が定義部分である。
Shapeデータとしてthis.generalPathを返せばよい。
|
具体例:RoundRectangle2DEのコンストラクタ
public RoundRectangle2DE(double x, double y, double width, double height,
double arcw, double arch){
this.x=x; this.y=y; this.width=width; this.height=height;
this.arcw=arcw; this.arch=arch;
this.generalPath=new GeneralPath();
this.segments=new Segment2D[8];
Line2D line0=new Line2D.Double(x, y+0.5*arch, x, y+height-0.5*arch);
Line2D line1=new Line2D.Double(x+0.5*arcw, y+height, x+width-0.5*arcw, y+height);
Line2D line2=new Line2D.Double(x+width, y+height-0.5*arch, x+width, y+0.5*arch);
Line2D line3=new Line2D.Double(x+width-0.5*arcw, y, x+0.5*arcw, y);
Arc2D arc0=new Arc2D.Double(x, y+height-arch, arcw, arch, 180, 90, Arc2D.OPEN);
Arc2D arc1=new Arc2D.Double(x+width-arcw, y+height-arch, arcw, arch, 270,
90, Arc2D.OPEN);
Arc2D arc2=new Arc2D.Double(x+width-arcw, y, arcw, arch, 0, 90, Arc2D.OPEN);
Arc2D arc3=new Arc2D.Double(x, y, arcw, arch, 90, 90, Arc2D.OPEN);
segments[0]=new Segment2D(Segment2D.LINE, line0);
segments[1]=new Segment2D(Segment2D.ARC, arc0);
segments[2]=new Segment2D(Segment2D.LINE, line1);
segments[3]=new Segment2D(Segment2D.ARC, arc1);
segments[4]=new Segment2D(Segment2D.LINE, line2);
segments[5]=new Segment2D(Segment2D.ARC, arc2);
segments[6]=new Segment2D(Segment2D.LINE, line3);
segments[7]=new Segment2D(Segment2D.ARC, arc3);
for(int i=0;i<segments.length;i++){
Shape shape=segments[i].getShape();
generalPath.append(shape,true);
}
generalPath.closePath();
}
4. Curve2D抽象クラス
戻る=>page top
public abstract class Curve2D
パラメトリック曲線定義の基となる抽象クラス。他のパラメトリック曲線はCurve2Dの拡張クラスとして宣言する。
|
フィールド
|
説明
|
|
segments
|
Segment2D[] segments
このパラメトリック曲線を構成するSegment2Dオブジェクトを設定する。
|
|
generalPath
|
GeneralPath generalPath
segmentsの各々に設定するjava.awt.Shapeデータ(Line2D, Arc2D, CubicCurve2D)をgeneralPath設定して、
Curve2D拡張クラスのShapeデータを作成する。この処理はCurve2D拡張クラスのコンストラクタで行う。
 =>
java.awt.Shapeデータの作成と取り出し =>
java.awt.Shapeデータの作成と取り出し
|
|
closed
|
boolean closed
閉曲線のときtrueを設定する。
|
|
Curve2D拡張クラスを表す定数
|
public static final int RECTANGLE=1, ROUND_RECTANGLE=2, ELLIPSE=3, LINE=4,
POLYLINE=5, CUBIC_CURVE=6, GENERAL_CURVE=7
GENERAL_CURVEは任意の曲線セグメントを任意個数接続した曲線のことである。
|
|
その他のstatic定数
|
double eps=1e-5, largeNumber=1e+5など
|
|
メソッド
|
説明
|
|
コンストラクタ
|
public Curve2D(Segment2D[] segments)
Segment2Dの配列を引数で渡してCurve2Dオブジェクトを作成する。
this.segments=segments;
this.generalPath=new GeneralPath();
Point2D startP=segments[0].getP(0);
Point2D endP=segments[segments.length-1].getP(1);
double dist=Vector2D.dist(new Vector2D(startP), new Vector2D(endP));
this.closed=false;
if(dist<Curve2D.eps) closed=true;
for(int i=0;i<segments.length;i++) {
Shape shape=segments[i].getShape();
this.generalPath.append(shape,true);
}
if(this.closed) this.generalPath.closePath();
|
|
setData
|
public void setData(Segment2D[] segments)
コンストラクターと同じ処理を行う。
|
|
getType2DE
|
public abstract int getType2DE()
パラメトリック曲線の種類を問い合わせる。定数RECTANGLE、ROUND_RECTANGLE…などが返される。
|
|
getShape
|
ppublic Shape getShape()
フィールド変数generalPathを返す。
 =>
java.awt.Shapeデータの作成と取り出し =>
java.awt.Shapeデータの作成と取り出し
|
| isClosed |
public boolean isClosed()
closed フィールドを返す。 |
|
getNumOfSegments
|
public int getNumOfSegments()
曲線セグメントの個数を返す。
|
|
getSegment2Ds
|
public Segment2D[] getSegment2Ds()
全ての曲線セグメントを返す。
|
|
getSegment2D
|
public Segment2D getSegment2D(int Index)
index番目の曲線セグメントを返す。
|
getP
|
public abstract Point2D getP(double t)
曲線パラメータtの点を計算して返す。
|
getTangent
|
public abstract Vector2D getTangent(double t)
曲線パラメータtでの接ベクトルを計算して返す。
|
| getTangentDerivative |
public Vector2D getTangentDerivative(double t)
曲線パラメータtでの2次微分ベクトルを返す。
|
| getEndPoints |
public Point2D[] getEndPoints()
始終点を返す。
|
| getCharacteristicPoints |
public CurvePT[] getCharacteristicPoints()
このオブジェクトの特徴点を返す。特徴点とは直線/曲線セグメントの始点、終点。中央点、そして円/楕円の東西南北点である。
 =>
ConnectionLS 図1 =>
ConnectionLS 図1
|
getCurveLength
|
public abstract double getCurveLength(double t1, double t2)
抽象メソッド。t1,t2区間の曲線長を返す。
|
|
getBoundingBox
|
public Rectangle2D getBoundingBox()
抽象メソッド。パラメトリック曲線全体を囲むBounding Boxを返す。
|
|
getBoundingBox
|
public Rectangle2D getBoundingBox(double t1, double t2)
抽象メソッド。パラメトリック曲線の部分区間を囲むBounding Boxを返す。
|
getSerializableCurve2D
|
public abstract SerializableCurve2D getSerializableCurve2D()
抽象メソッド。ファイルに書き込むためのデータを取り出す。
SerializableCurve2DはCurve2Dの拡張クラスのデータ部分だけを取り出したクラスでSerializableElementと同様な役割を果たす。
 =>
SerializableElement =>
SerializableElement
|
| setSerializableCurve2D |
public void setSerializableCurve2D(SerializableCurve2D sdata)
引数:
sdata- SerializableCurve2Dオブジェクト。
ファイル書き込みに使われる形式。
処理:
sdataの内容をこのオブジェクトに設定する。
|
convertToGeneral
Curve2DE
|
public GeneralCurve2DE convertToGeneralCurve2DE()
GeneralCurve2DEに変換する。
定型的なRectangle2DE, RoundRectangle2DE...などに回転を加えるとき、GeneralCurve2DEの変換してから行う。
|
| reverse |
public void reverse()
このオブジェクトの曲線の方向を反転する。Segment2D.reverseSegmentメソッドを使う。. |
| transform |
public void transform(Matrix2D M)
引数:
M- 変換マトリックス.
処理:
このオブジェクトの曲線をマトリックスをで変換する。
Segment2D.transformSegmentメソッドを使う。
|
clone
(abstract)
|
public abstract Object clone()
複製を作る。
|
toString
(abstract)
|
public abstract String toString()
文字列表現を返す。
|
5. Rectangle2DE(Curve2D拡張クラス)
戻る=>page top
public class Rectangle2DE extends Curve2D
java.awt.geom.Rectangle2Dにパラメトリック曲線の機能を加えたクラス。
|
メソッド
|
説明
|
| コンストラクタ |
Rectangle2DE(Segment2D[] segments)
Curve2D constructorを呼ぶ。
|
|
コンストラクタ
|
public Rectangle2DE(double x, double y, double width, double height)
Line2Dセグメントを各4本接続して作成する。
引数はjava.awt.geom.Rectangle2D.Double同じ。
|
|
getType2DE
|
public int getType2DE()
定数Curve2D.RECTANGLEを返す。
|
|
getX
|
public double getX():Rectangle2DE固有メソッド
java.awt.geom.Rectangle2Dの同名メソッドと同じ。矩形データの左上隅点のX座標を返す。
|
|
getY
|
public double getY():Rectangle2DE固有メソッド
矩形データの左上隅点のY座標を返す。
|
|
getWidth
|
public double getWidth():Rectangle2DE固有メソッド
矩形データの幅を返す。
|
|
getHeight
|
public double getHeight():Rectangle2DE固有メソッド
矩形データの高さを返す。
|
|
clone
|
public Object clone()
コンストラクタを使って新しいオブジェクトを作成する。
|
|
toString
|
public String toString()
|
6. RoundRectangle2DE(Curve2D拡張クラス)
戻る=>page top
public class RoundRectangle2DE extends Curve2D
java.awt.geom.RoundRectangle2Dにパラメトリック曲線の機能を加えたクラス。
|
メソッド
|
説明
|
| コンストラクタ |
RoundRectangle2DE(Segment2D[] segments)
Curve2D constructorを呼ぶ。
|
|
コンストラクタ
|
public RoundRectangle2DE(double x, double y, double width, double height,
double arcw, double arch)
Line2D、Arc2Dのセグメントを各4本接続して作成する。
引数はjava.awt.geom. RoundRectangle2D.Double同じ。
|
|
setData
|
public void setData(double x, double y, double width, double height, double
arcw, double arch)
コンストラクタと同じ処理。
|
|
getType2DE
|
public int getType2DE()
定数Curve2D.ROUND_RECTANGLEを返す。
|
|
getX
|
public double getX() :RoundRectangle2DE固有メソッド
java.awt.geom.RoundRectangle2Dの同名メソッドと同じ。矩形データの左上隅点のX座標を返す。
|
|
getY
|
public double getY() :RoundRectangle2DE固有メソッド
矩形データの左上隅点のY座標を返す。
|
|
getWidth
|
public double getWidth() :RoundRectangle2DE固有メソッド
矩形データの幅を返す。
|
|
getHeight
|
public double getHeight() :RoundRectangle2DE固有メソッド
矩形データの高さを返す。
|
|
getArcWidth
|
public double getArcWidth() :RoundRectangle2DE固有メソッド
コーナーARCの幅を返す。
|
|
getArcHeight
|
public double getArcHeight() :RoundRectangle2DE固有メソッド
コーナーARCの高さを返す。
|
|
clone
|
public Object clone()
|
|
toString
|
public String toString()
|
7. Ellipse2DE(Curve2D拡張クラス)
戻る=>page top
public class Ellipse2DE extends Curve2D
java.awt.geom.Ellipse2Dにパラメトリック曲線の機能を加えたクラス。
|
メソッド
|
説明
|
| コンストラクタ |
Ellipse2DE(Segment2D[] segments)
Curve2D constructorを呼ぶ。
|
|
コンストラクタ
|
public Ellipse2DE(double x, double y, double width, double height)
Arc2Dセグメント一個で作成する。
引数はjava.awt.geom. Ellipse2D.Double同じ。
|
|
getType2DE
|
public int getType2DE()
定数Curve2D.ELLIPSEを返す。
|
|
getX
|
public double getX() :Ellipse2DE固有メソッド
java.awt.geom.Ellipse2Dの同名メソッドと同じ。Ellipse2Dを囲む矩形データの左上隅点のX座標を返す。
|
|
getY
|
public double getY() :Ellipse2DE固有メソッド
Ellipse2Dを囲む矩形データの左上隅点のY座標を返す。
|
|
getWidth
|
public double getWidth() :Ellipse2DE固有メソッド
Ellipse2Dを囲む矩形データの幅を返す。
|
|
getHeight
|
public double getHeight() :Ellipse2DE固有メソッド
Ellipse2Dを囲む矩形データの高さを返す。
|
|
clone
|
public Object clone()
|
|
toString
|
public String toString()
|
8. Line2DE(Curve2D拡張クラス)
戻る=>page top
public class Line2DE extends Curve2D
java.awt.geom.Line2Dにパラメトリック曲線の機能を加えたクラス。
|
メソッド
|
説明
|
| コンストラクタ |
Line2DE(Segment2D[] segments)
Curve2D constructorを呼ぶ。
|
|
コンストラクタ
|
Line2DE(Point2D p1, Point2D p2)
LINE2Dセグメント一個で作成する。
引数はjava.awt.geom.Line2D.Double同じ。
|
|
setData
|
public void setData(Point2D p1, Point2D p2)
コンストラクタと同じ処理。
|
|
getType2DE
|
public int getType2DE()
定数Curve2D.LINEを返す。
|
|
getP1
|
public Point2D getP1() :Line2DE固有メソッド
直線の始点を返す。
|
|
getP2
|
public Point2D getP2() :Line2DE固有メソッド
直線の終点を返す。
|
|
getX1
|
public double getX1() :Line2DE固有メソッド
直線の始点のx座標を返す。
|
|
getY1
|
public double getY1() :Line2DE固有メソッド
直線の始点のy座標をを返す。
|
|
getX2
|
public double getX2() :Line2DE固有メソッド
直線の終点のx座標を返す。
|
|
getY2
|
public double getY2() :Line2DE固有メソッド
直線の終点のy座標を返す。
|
| getTrimmedCurve2D |
public Line2DE getTrimmedCurve2D(double t1, double t2)
このパラメトリック曲線の[t1,t2]区間の直線を返す。
|
| getTrimmedLine |
public Line2DE getTrimmedLine(double cut1, double cut2)
getTrimmedCurve2Dと同様。引数が曲線パラメータではなくピクセル単位の切断量で与えられる。
このメソッドは現在のところ、DrawShapeUtil.getTrimmedLineから呼ばれ、矢印を描画する線分の先端をカットするのに使われている。 |
|
clone
|
public Object clone()
|
|
toString
|
public String toString()
|
9. Polyline2DE(Curve2D拡張クラス)
戻る=>page top
public class Polyline2DE extends Curve2D
直線セグメントを接続した折れ線のパラメトリック曲線。
|
メソッド
|
説明
|
|
コンストラクタ
|
public Polyline2DE(Segment2D[] segments)
Curve2D constructorを呼ぶ。
|
|
コンストラクタ
|
public Polyline2DE(Point2D[] points)
点列データから折れ線データを作成する。
|
|
コンストラクタ
|
public Polyline2DE(Point2D[] points, boolean closed)
処理は同上。閉じた折れ線かどうかは引数closedで指定する。
|
|
setData
|
public void setData(Point2D[] points, boolean closed) :Polyline2DE固有メソッド
コンストラクタと同じ処理。
|
|
setData
|
public void setData(Point2D[] points) :Polyline2DE固有メソッド
コンストラクタと同じ処理。
|
|
getType2DE
|
public int getType2DE()
定数Curve2D.POLYLINEを返す。
|
|
getPoints
|
public Point2D[] getPoints():Polyline2DE固有メソッド
折れ線の節点列を返す。
|
|
getPoint
|
public Point2D getPoint(int index) :Polyline2DE固有メソッド
指定された番号の節点を返す。
|
|
getTrimmedCurve2D
|
public Polyline2DE getTrimmedCurve2D(double t1, double t2) :Polyline2DE固有メソッド
折れ線の曲線パラメータt1,t2区間の折れ線を返す。
|
| getTrimmedPolyline |
public Polyline2DE getTrimmedPolyline(double cut1, double cut2) :Polyline2DE固有メソッド
getTrimmedCurve2Dと同様。引数が曲線パラメータではなくピクセル単位の切断量で与えられる。
このメソッドは現在のところ、DrawShapeUtil.getTrimmedLineから呼ばれ、矢印を描画する線分の先端をカットするのに使われている。 |
|
clone
|
public Object clone()
|
|
toString
|
public String toString()
|
10. CubicCurve2DE(Curve2D拡張クラス)
戻る=>page top
public class CubicCurve2DE extends Curve2D
三次曲線要素(CubicCurve2D)を接続したパラメトリック曲線。
|
メソッド
|
説明
|
|
コンストラクタ
|
public CubicCurve2DE(Segment2D[] segments)
Curve2D constructorを呼ぶ。
|
|
コンストラクタ
|
public CubicCurve2DE(Point2D[] Q)
制御点列Qからn本のCubicCurve2Dセグメントを作成する。点列の数は3*n+1個。
|
|
setData
|
public void setData(Point2D[] points) ;CubicCurve2DE固有メソッド
コンストラクタと同じ処理。
|
|
getType2DE
|
public int getType2DE()
定数Curve2D.CUBIC_CURVEを返す。
|
|
getPoints
|
public Point2D[] getPoints() ;CubicCurve2DE固有メソッド
三次曲線の節点列を返す。節点は三次曲線要素の端点であり、(曲線要素数+1)個の節点が返される。
|
|
getCtrlPoints
|
public Point2D[] getCtrlPoints() ;CubicCurve2DE固有メソッド
三次曲線の制御点列を返す。制御点列はCubicCurve2DE(Point2D[] Q)の引数と同じ形式で、(3×曲線要素数+1)個の制御点列が返される。
|
|
getFergusonCurve2D
|
public FergusonCurve2D getFergusonCurve2D() ;CubicCurve2DE固有メソッド
三次曲線をFergusonCurve2D形式に変換して返す。
|
|
getTin
|
public Vector2D getTin(int index) ;CubicCurve2DE固有メソッド
節点の+側の接ベクトルを返す。
|
|
getTout
|
public Vector2D getTout(int index) ;CubicCurve2DE固有メソッド
節点の-側の接ベクトルを返す。一般的にTinとToutの方向は同じであるが、ベクトル長は異なる。
|
|
getTrimmedCurve2D
|
public CubicCurve2DE getTrimmedCurve2D(double t1, double t2) ;CubicCurve2DE固有メソッド
曲線パラメータt1,t2区間の三次曲線を返す。
CubicCurveElement.getTrimmedCubicCurveから呼ばれる。曲線の両端に矢印を表示する場合などに使う。
|
|
clone
|
public Object clone()
|
|
toString
|
public String toString()
|
11. GeneralCurve2DE(Curve2D拡張クラス)
戻る=>page top
public class GeneralCurve2DE extends Curve2D
任意の曲線セグメントを接続したパラメトリック曲線。
曲線の切断・接続、図形の回転などで作成される曲線を表すのに使う。
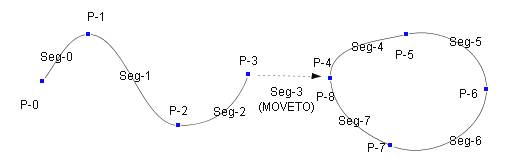
図 11.1 グローバルなセグメント番号, セグメント接続点番号
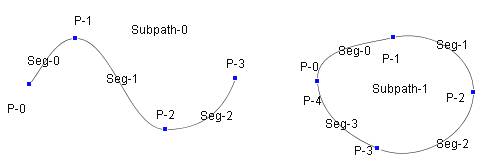
図 11.2 サブパスごとのセグメント番号, セグメント接続点番号
サブパスごとに0から番号づけられる |
(a) 0-7セグメントの表示
segment[0]=CUBIC, P1=640.04,371.28, P2=685.90,324.95, CtrlP1=654.01,353.07,CtrlP2=665.80,324.95
segment[1]=CUBIC, P1=685.90,324.95, P2=775.45,415.98, CtrlP1=722.90,324.95, CtrlP2=738.46,415.93
segment[2]=CUBIC, P1=775.45,415.98, P2=846.18,364.98, CtrlP1=801.94,416.01, CtrlP2=831.32,406.89
segment[3]=MoveTo
segment[4]=CUBIC, P1=928.82,371.58, P2=1,004.96,328.01, CtrlP1=926.56,337.66, CtrlP2=975.82,334.84
segment[5]=CUBIC, P1=1,004.96,328.01, P2=1,085.27,382.36, CtrlP1=1,041.93,319.35, CtrlP2=1,086.01,344.76
segment[6]=CUBIC, P1=1,085.27,382.36, P2=989.42,438.44, CtrlP1=1,084.42,425.39, CtrlP2=1,029.39,455.40
segment[7]=CUBIC, P1=989.42,438.44, P2=928.82,371.58, CtrlP1=960.27,426.07, CtrlP2=931.06,405.02
(2) 0-7セグメントをサブパス形式で表示
- sub path=0, close=false, numseg=3, startSegment=0, endSegment=2 [ start t-param=0, end t-param=3 ]
segment[0]=CUBIC, P1=640.04,371.28, P2=685.90,324.95, CtrlP1=654.01,353.07, CtrlP2=665.80,324.95
segment[1]=CUBIC, P1=685.90,324.95, P2=775.45,415.98, CtrlP1=722.90,324.95, CtrlP2=738.46,415.93
segment[2]=CUBIC, P1=775.45,415.98, P2=846.18,364.98, CtrlP1=801.94,416.01, CtrlP2=831.32,406.89
- sub path=1, close=true, numseg=4, startSegment=4, endSegment=7 [ start t-param=4, end t-param=8 ]
segment[0]=CUBIC, P1=928.82,371.58, P2=1,004.96,328.01, CtrlP1=926.56,337.66, CtrlP2=975.82,334.84
segment[1]=CUBIC, P1=1,004.96,328.01, P2=1,085.27,382.36, CtrlP1=1,041.93,319.35, CtrlP2=1,086.01,344.76
segment[2]=CUBIC, P1=1,085.27,382.36, P2=989.42,438.44, CtrlP1=1,084.42,425.39, CtrlP2=1,029.39,455.40
segment[3]=CUBIC, P1=989.42,438.44, P2=928.82,371.58, CtrlP1=960.27,426.07, CtrlP2=931.06,405.02
|
|
メソッド
|
説明
|
|
コンストラクタ
|
public GeneralCurve2DE(Segment2D[] segments)
次のsetDataメソッドを呼ぶ。
|
| setData |
public void setData(Segment2D[] segments)
セグメント(Segment2D オブジェクト)を設定する。
図11.1の例ではMOVETOセグメントを含む8個のセグメントを設定する。
|
|
getType2DE
|
public int getType2DE()
定数Curve2D.GENERAL_CURVEを返す。
|
| getNumOfSubPaths |
public int getNumOfSubPaths()
サブパス数を返す。図11.1の例では2。
|
| getNumOfLocalSegments |
public int[] getNumOfLocalSegments()
サブパスのセグメント数を配列返す。図11.1の例ではint[0]=3, int[0]=4。 |
| getSubPathIndex |
public int getSubPathIndex(int segmentPtIndex)
セグメント番号、セグメント接続点番号を渡し、サブパス番号を返す。
図11.1の例ではsegmentPtIndex=0∽3=>SubPathIndex=0, segmentPtIndex=4∽8=>SubPathIndex=2。
|
| getLocalSegmentIndex |
private int getLocalSegmentIndex(int segmentIndex)
セグメント番号を渡し、サブパスでのセグメント番号を返す
図11.1の例では次のようになる。
∙ segmentIndex=0∽2=>localSegmentIndex=0∽2,
∙ segmentIndex=4∽7=>localSegmentIndex=0∽3,
∙ segmentIndex=3=>localSegmentIndex=-1(MOVETOセグメントなので無効)
|
| getLocalSegmentPtIndex |
public int getLocalSegmentPtIndex(int segmentPtIndex)
セグメント番号を渡し、サブパスでのセグメント番号を返す
図11.1の例では次のようになる。
∙ segmentPtIndex=0∽3=>localSegmentPtIndex=0∽3.
∙ segmentPtIndex=4∽8=>localSegmentPtIndex=0∽4.
|
| getGlobalSegmentIndex |
private int getGlobalSegmentIndex(int subPathIndex, int localSegmentIndex)
サブパス番号とサブパスでのセグメント番号を渡し、グローバルなセグメント番号を返す
図11.1の例では次のようになる。
∙ subPathIndex=0, localSegmentIndex=0∽2=>globalSegmentIndex=0∽2.
∙ subPathIndex=1, localSegmentIndex=0∽3=>globalSegmentIndex=4∽7.
∙ 上記以外は-1(無効)を返す
|
| getGlobalSegmentPtIndex |
public int getGlobalSegmentPtIndex(int subPathIndex, int localSegmentPtIndex)
サブパス番号とサブパスでのセグメント番号またはセグメント接続点番号を渡し、グローバルなセグメント番号を返す
図11.1の例では次のようになる。
∙ subPathIndex=0, localSegmentPtIndex=0∽3=>globalSegmentPtIndex=0∽3.
∙ subPathIndex=1, localSegmentPtIndex=0∽4=>globalSegmentPtIndex=4∽8.
∙ 上記以外は-1(無効)を返す.
|
| getSubPathSegments |
private Segment2D[] getSubPathSegments(int subPathIndex)
サブパス番号を指定し、そのサブパスのセグメントを返す。
図11.1の例ではsubPathInde=0ならば0∽2セグメントを、subPathInde=1ならば4∽7セグメントを返す。
|
| getSubPath |
private GeneralCurve2DE getSubPath(int index)
サブパス番号を指定し、そのサブパスをGeneralCurve2DE形式で返す。
図11.1の例ではsubPathInde=0ならば0∽2セグメントを含むGeneralCurve2DEを、
subPathInde=1ならば4∽7セグメントを含むGeneralCurve2DEを返す。
|
| getSubPaths |
public GeneralCurve2DE[] getSubPaths()
サブパスをGeneralCurve2DE形式の配列で返す。
|
| setSubPaths |
public void setSubPaths(Curve2D[] curves)
複数のサブパスを渡し、このGeneralCurve2DEオブジェクトにセグメントを設定する。
∙ サブパス間の接続をPathConnectクラスでテストし、
接続できればサブパスを一本にまとめて登録する。
|
| isClosed |
public boolean isClosed()
サブパスが一本でそのサブパスが閉曲線ならばtrueを返し、それ以外はfalseを返す。
個々のサブパスの開/閉は、getSubPathsメソッドでサブパスの曲線データを取得しisClose()メソッドで問い合わせる。
|
|
getTrimmedCurve2D
|
public CubicCurve2DE getTrimmedCurve2D(double t1, double t2) ;GeneralCurve2DE固有メソッド
曲線パラメータt1,t2区間の三次曲線を返す。
CubicCurveElement.getTrimmedCubicCurveから呼ばれる。曲線の両端に矢印を表示する場合などに使う。
|
| getSimpleCurve2Ds |
public Curve2D[] getSimpleCurve2Ds() |
| getSimpleCurve2D |
public Curve2D getSimpleCurve2D(double t1, double t2) :GeneralCurve2DE固有メソッド
より簡単な形式のパラメトリック曲線に変換して返す。たとえば曲線セグメントが全て直線で構成されているときは、Line2DEまたはPolyline2DEを返すなど。
このメソッドは曲線の接続(ConnectCurves)などで、接続曲線をGeneralCurve2D形式で作成するが、より簡単な形式で表せるときに使う。 |
|
clone
|
public Object clone()
|
|
toString
|
public String toString()
|
12. FergusonCurve2D
戻る=>page top
public class FergusonCurve2D
Curve2Dの拡張クラスではない。三次曲線のFerguson曲線形式。
CubicCurve2DEは接線ベクトルの扱いが直感的ではないので、ほとんどFergusonCurve形式で処理する。
FergusonCurveは節点データと節点でのプラス側、マイナス側の接ベクトルTin(C'
(t-0))、Tout(C'(t+0))を持つ形式である。
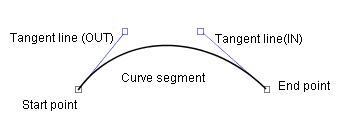
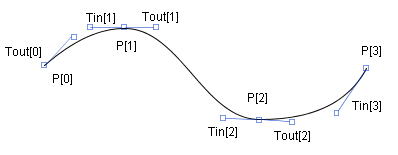 Figure 12.1 Ferguson曲線
Figure 12.1 Ferguson曲線
|
メソッド
|
説明
|
|
コンストラクタ
|
public FergusonCurve2D()
データのないFergusonCurve2Dオブジェクトを作成する。
|
|
コンストラクタ
|
public FergusonCurve2D(Point2D[] P, Vector2D[] Tin, Vector2D[] Tout)
節点の位置データ、マイナス側、プラス側接ベクトルを引数で渡し、FergusonCurve2Dオブジェクトを作成する。
pの個数がnでP[0}=P[n-1]の場合はclosed=true。
|
|
isClosed
|
public boolean isClosed()
閉曲線のときtrueを返す。
|
|
getNumOfSegments
|
public int getNumOfCSegments()
FergusonCurveセグメント数を返す。
|
|
getCubicCurve2DE
|
public CubicCurve2DE getCubicCurve2DE()
FergusonCurve2DをCubicCurve2DE形式に変換して返す。
|
|
getCubicCurve2D
|
public CubicCurve2D getCubicCurve2D(int index)
index番目のFergusonCurveセグメントをjava.awt.geom.CubicCurve2D形式(Bezier曲線要素)に変換して返す。
|
|
getCtrlPoints
|
public Point2D[] getCtrlPoints()
FergusonCurve2DをCubicCurve2DE形式に変換し制御点列を返す。
制御点列はCubicCurve2DE(Point2D[] Q)の引数と同じ形式で、(3×曲線要素数+1)個。
|
|
getP
|
public Point2D getP(int index)
index番目の節点を返す。
|
|
setP
|
public void setP(Point2D P, int index)
index番目の節点をセットする。
|
|
getTin
|
public Vector2D getTin(int index)
index番目の節点のマイナス側接ベクトル(C'(index-0)を返す。
|
|
setTin
|
public void setTin(Vector2D Tin, int index)
index番目の節点のマイナス側接ベクトルを設定する。
|
|
getTout
|
public Vector2D getTout(int index)
index番目の節点のプラス側接ベクトル(C'(index+0)を返す。
|
|
setTout
|
public void setTout(Vector2D Tout, int index)
index番目の節点のプラス側接ベクトルを設定する。
|
|
getP
|
public Point2D getP(double t)
曲線パラメータtでの曲線上の点を返す。
|
|
getTangent
|
public Vector2D getTangent(double t)
曲線パラメータtでの接ベクトルを返す。
|
|
movePoint
|
public void movePoint(int index, Point2D newPoint)
引数:
index- The index of the segment junction point.
newPoint- the new segment junction point.
処理:
indexの節点位置をnewPointで置き換える。[index-1, index]区間, [index,index+1]区間の接ベクトルの方向は変えないが、長さを変えて最適化する。接ベクトル長は円弧を最適近似する長さに変える(getOptimizedTangents)。もちろんindexが始点を指すときは[index-1,
index]区間は処理しないし、indexが終点を指すときは[index, index+1]区間は処理しない。
閉曲線でindexが始点または終点を指すときは次のように処理する。セグメント数をnsegとする。
・始点、終点にsetPメソッドでnewPointを設定。setP(newPoint, 0), setP(newPoint, nseg)。
・[nseg-1, nseg]区間、[0, 1]区間の接ベクトル長を
getOptimizedTangentsで変える。
|
|
moveTangent
|
public void moveTangent(int index, Vector2D newTangent)
引数:
index- The index of the segment junction point.
newTangent- The new tangent vector.
The direction of the newTangent will be referred (the length isn't referred).
処理:
indexの位置のTin, ToutをnewTangentで置き換える。
[index-1, index]区間, [index,index+1]区間の接ベクトルの長さを変えて最適化する
(getOptimizedTangents)。
閉曲線の場合の処理を含め、接ベクトルの設定処理はmovePointと同じ。
|
|
addPoint
|
public void addPoint(double t)
曲線パラメータtの位置に新しい節点を追加する。tの両側の節点パラメータはit=(int)tとit+1。
節点を追加した後は、itが追加された節点の手前の番号、it+1が追加された節点の番号となる。
it節点のToutベクトル、it+1節点のTin, Toutベクトル、it+2節点のTinベクトルの方向は変わらないが、
長さを変えなければならない。
・Tout(it), Tin(it+1):元のTout,Tinの長さを(t-it)倍
・Tout(it+1), Tin(it+2):元のTout,Tinの長さを(it+1-t)倍
|
|
deletePoint
|
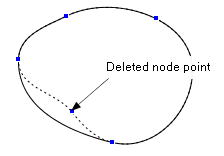
public void deletePoint(int index)
index番目の節点を削除する。閉曲線の場合、始点と終点は重なっているので注意。
・節点、接ベクトルを格納する配列newP, newTout, newTinを確保。配列のサイズは現在の配列サイズ-から1減らす。
・index番目を除いたデータをnewP, newTout, newTinに設定。
閉曲線で始点または終点を削除するときは、始点側のデータを除いてnewP, newTout, newTinに設定する(*1)。
削除された点は、新しいnewP, newTout, newTinの[index-1,index]区間にあった(但しindexが始終点以外の場合)。
・[index-1,index]区間の接ベクトル(newTout[index-1]とnewTin[index])の長さを変更する。
getOptimizedTangentsで新しい接ベクトルを取得しnewTout[index-1]とnewTin[index]に設定する。
・閉曲線でindexが始点または終点を指している場合。
(*1)ため、newP[0]は削除された始点の次の点、newP[np-1]には削除された点の座標が入っている(npはnewPの配列数)。
newP[0]->newP[np-1]。newTout[0]->newTin[np-1]。
削除された点は[np-2,np-1]区間にあったので、この区間の接ベクトル長をgetOptimizedTangentsで変更する。
|
|
toString
|
public String toString()
FergusonCurve2Dの文字列表現を返す。
|
createNaturalSpline
(static)
|
public static FergusonCurve2D createNaturalSpline(Point2D[] nodePTs)
通過点を通るC2級のスプライン曲線を生成する。始点、終点での接線方向を点を通過する円弧から決め、
連立方程式を解いて各節点での接ベクトル方向を決める。
接ベクトル長はcreateArcApproximatedCurveメソッドと同様、3点を通過する円弧から決める。
|
getUnitTangentOfOpen
Curve
(static)
|
public static Vector2D[] getUnitTangentOfOpenCurve(Point2D[] nodePTs)
開いた曲線の各節点での単位接ベクトルを連立方程式から計算する。接ベクトル長は引数arcLengthで与える。
連立方程式の数は通過点の個数と同じ。
|
getUnitTangentOfClosed
Curve
(static)
|
public static Vector2D[] getUnitTangentOfClosedCurve(Point2D[] nodePTs)
閉じた曲線の各節点ので単位接ベクトルを連立方程式から計算する。
通過点の個数をnとすると連立方程式の数は(n-1)個。但し、閉じた曲線の場合passingP[0]=passingP[n-1]なので、
重複をカウントしなければ通過点の個数と同じである。
|
getOptimizedTangents
(static)
|
public static Vector2D[] getOptimizedTangents(Point2D P0, Point2D P1, Vector2D Tout, Vector2D Tin)
引数:
P0- 始点
P1- 終点
Tout- 始点での接ベクトル
Tin- 終点での接ベクトル
戻り値:
Tout, Tinの長さを最適化して返す。
処理:
下図の記号
⋅ 直線P0,Q0:Toutに垂直な直線。
⋅ 直線P1,Q1: Tinに垂直な直線。
⋅ 点P01:P0, P1の中点。
⋅ 直線P01, Q1:直線P0, P1に垂直な直線。
Tout, Tinの最適化した長さ|Tout|, |Tin|は次のように計算する。
|Tout|=4.0*r0*(1-cos(teta0))/sin(teta0)
|Tin| =4.0*r1*(1-cos(teta1))/sin(teta1)
|Tout|はQ0を中心とする中心角tete0の円弧を最適近似する長さ、
|Tin|はQ1を中心とする中心角tete1の円弧を最適近似する長さである。
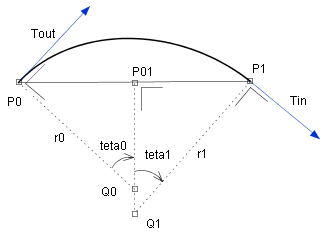
 :Tout、Tinが平行のときは、
直線P0, P1の長さにする。 :Tout、Tinが平行のときは、
直線P0, P1の長さにする。
|
|
![]()
![]()
![]()
![]()
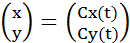 (式1)
(式1) =>
java.awt.geomの機能拡張
=>
java.awt.geomの機能拡張 :getShapeの特別なケース
:getShapeの特別なケース