要旨:Curve2DUtilはパラメトリック曲線間の交点計算、点からパラメトリック曲線へ最短点計算などのメソッドを集めたクラス。メソッドは全てstaticメソッド。CrossCurvePTはパラメトリック曲線間の交点を表すクラス、CurvePTはパラメトリック曲線上の点を表すクラスで、(x,y)の他に曲線パラメータを持つ。
Curve2DUtilは本体で、曲線間の交点計算、点から曲線への垂線計算、最短点計算などのメソッドを集めたクラス。
Newton-Raphson法を使うので信頼性のテストができるコマンドを用意している。
 =>操作説明書 テスト =>操作説明書 テスト
Vector2Dはベクトル計算のメソッドを集めたクラス、 Matrix2Dはマトリックス作成や演算のクラス、Matrixはガウス消去法のクラスで節点列が与えられた時に自然スプラインを作成するために使う。
|
| このページで説明するクラス:
CrossCurvePT, CurvePT,
Curve2DUtil, Vector2D,
Matrix2D, Matrix |
 =>DrawTest: 任意2曲線の交点計算,
曲線への垂線の計算
任意2曲線への共通垂線計算
=>DrawTest: 任意2曲線の交点計算,
曲線への垂線の計算
任意2曲線への共通垂線計算
1. CrossCurvePTクラス
public class CrossCurvePT
曲線間の交点を表すクラスで、曲線1のパラメータt1とその点p1、曲線2のパラメータt2とその点p2を持つ。
フィールド
|
説明
|
t1
|
public double t1: 曲線1のパラメータt1
|
t2
|
public double t2: 曲線2のパラメータt2
|
p1
|
Point2D p1:パラメータt1での曲線1上の点。
|
p2
|
Point2D p2:パラメータt2での曲線2上の点。
|
|
メソッド
|
説明
|
コンストラクタ
|
public CrossCurvePT(double t1, double t2, Point2D p1, Point2D p2)
引数の意味はフィールドを参照。
|
getParameterT1
|
public double getParameterT1():t1を返す。
|
getParameterT2
|
public double getParameterT2():t2を返す。
|
getP1
|
public Point2D getP1():p1を返す。
|
getP2
|
public Point2D getP2():p2を返す。
|
getCurvePT
|
public CurvePT getCurvePT(int index)
CurvePTに変換して返す。
index=0ならば曲線1上のCurvePT、index=1ならば曲線2上のCurvePTの変換。
|
exchangeData
|
public CrossCurvePT exchangeData()
t1,t2およびp1,p2を交換したCrossCurvePTを返す。
|
toString
|
public String toString():文字列表現を返す。
|
2. CurvePTクラス戻る=>page top
public class CurvePT
曲線上の点を表すクラスで、曲線のパラメータtとその点pを持つ。staticメソッドgetNormalLines, getShortestNormalLine,
getShortestLineが返すデータは、CurvePTの配列である。
|
フィールド
|
説明
|
t
|
public double t: 曲線パラメータt
|
p
|
Point2D p: 曲線パラメータtでの点。
|
| curve |
Curve2D curve
pが乗っている Curve2Dオブジェクト。 |
|
メソッド
|
説明
|
コンストラクタ
|
public CrossCurvePT(double t, Point2D p)
引数の意味はフィールドを参照。
|
getParameter
|
public double getParameter ():tを返す。
|
getP
|
public Point2D getP1():pを返す。
|
| selectCurvePT |
public static CurvePT selectCurvePT(Point2D p, CurvePT[] curvePTs)
curvePTsから引数pに最も近いものを返す。
|
toString
|
public String toString():文字列表現を返す。
|
3. Curve2DUtilクラス
戻る=>page top
public class Curve2DUtil
|
フィールド
|
説明
|
pai
|
final static double pai=Math.PI: π
|
largeNumber
|
final static double largeNumber=1e+5: 大きな値
|
eps10
|
final static double eps0=1e-10:収束判定に使う。曲線パラメータtに関する判定値。
|
eps4
|
final static double eps=1e-4:ピクセル座標での判定値。
|
eps3
|
final static double eps=1e-3:ピクセル座標での判定値。
|
publicメソッド一覧
3.1 任意2曲線間の交点
戻る=>Curve2DUtil
 計算式=>
NewtonRaphson法による交点計算方法 計算式=>
NewtonRaphson法による交点計算方法
メソッド
|
説明
|
getIntersectionPts
(static)
|
public static CrossCurvePT[] getIntersectionPts(Curve2D curve1, Curve2D curve2)
引数:
curve1 - 第1 Curve2D オブジェクト。
curve2 - 第2 Curve2D オブジェクト。
戻り値:
交点をCrossCurvePTオブジェクトの配列を返す。交点がないときは長さ0の配列を返す。
処理:
曲線間の交点計算を行う最上位メソッド。
曲線セグメントの組み合わせに分解して、下記のgetIntersectionPtsOfSegmentsメソッドを呼ぶ。
処理の終了前に、つぎのeliminateDuplicationAndSor メソッドを呼んで、出力データCrossCurvePT[]の重複チェックとソートを行う。ソートはCrossCurvePTのcurve1曲線パラメータの小さい順。
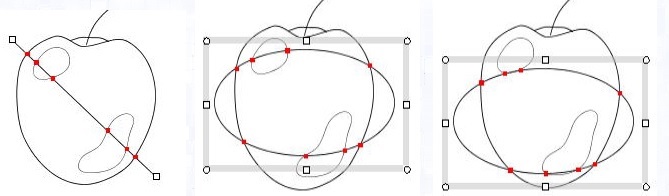
|
eliminateDuplication
AndSort
(static)
|
protected static CrossCurvePT[] eliminateDuplicationAndSort(CrossCurvePT[]
PTs, double tolerance)
引数PTsで与えられるデータの重複チェックを行い、曲線パラメータが近い点を削除する。
同時に曲線パラメータt1についてソートして出力する。
ソートはUtil.indexedSimpleSort を使う。
|
getIntersectionPtsOfSegments
(static)
|
private static CrossCurvePT[] getIntersectionPtsOfSegments(Segment2D segment1,
Segment2D segment2)
引数:
segment1 - 第1 Segment2D オブジェクト。
segment2 - 第2 Segment2D オブジェクト。
戻り値:
曲線セグメント間の交点を CrossCurvePT オブジェクトの配列を返す。
交点がないときは長さ0の配列を返す。
処理:
曲線セグメント間の交点を計算する。
①直線×直線、
②直線×楕円弧(java.awt.geom.Arc2D)
③楕円弧×楕円弧
④直線/楕円弧/三次曲線×三次曲線、
の組み合わせに分かれる。①, ②は初等計算式で解ける。
③の特殊ケース:円弧×円弧は初等計算式で解けるが、一般の楕円弧×楕円弧の場合は交点が4個になるので解けない。
また④は一般には初等計算式で解けない。以上のことから③, ④にはNewton-Raphson法を使う。
|
intersectionPtOfLines
(static)
|
private static CrossCurvePT intersectionPtOfLines(Segment2D segment1, Segment2D segment2)
引数, 戻り値はgetIntersectionPtsOfSegmentsと同じ。
直線セグメント×直線セグメントの交点計算。
|
intersectionPtsOfLineAndArc
(static) |
private static CrossCurvePT[] intersectionPtsOfLineAndArc(Segment2D segment1, Segment2D segment2)
引数, 戻り値はgetIntersectionPtsOfSegmentsと同じ。
処理:
直線セグメント×楕円弧セグメントの交点計算。
[計算式]
楕円弧の中心点をQ=(Qx, Qy), 長径をa, 短径をbとすると、楕円弧の式はつぎ。
(xーQx)2/a2 + (yーQy)2/b2 =1
(1)
また極座標系ではつぎ。
x = a*cosθ+Qx,y = - (b*sinθ+Qy)
(2)
ここでy座標の前のマイナス記号は、グラフィック座標系ではy軸が下向きであることを考慮した。
直線の始終点をp1=(p1x, p1y), p2=(p2x, p2y)とし、p1->p2ベクトルをT=(Tx, Ty)とすれば、
直線の式はパラメータtを使って次のように書ける。
x=Tx*t+p1x,y=Ty*t+p1y
(3)
(3)式を(1)式に代入し、P=(p1x-Qx, p1y-Qy)と記すとつぎ。
(Tx*t+Px)/2/a2 + (Ty*t+Py)/2/a2 = 1
(4)
これからパラメータ t を求める。(4)式はつぎように書ける。
c0*t2 + c1*t + c2 = 0(5)
ここで、
c0 = Tx2/a2 + Ty2/b2,
c1 = 2(Tx*Px/a2 + Ty*Py/b2),
c2 = Px2/a2 + Py2/b2 - 1
(5)式を解いて t が求まる。この t がCrossCurvePT オブジェクトに
セットする直線側のパラメータ t1 になる。
楕円弧側の曲線パラメータ t2 は(2)式から求める。
交点が2個求まったとしてPT1=(PT1x, PT1y), PT2=(PT2x, PT2y)と書くと, PT1については次式。
cosθ = (PT1x-Qx)/a, sinθ = - (PT1y-Qy)/b
これからθを求める。楕円弧側の曲線パラメータ t2 でθを書くと, θ = start*t2+ extent。
ここでstart, extentはARC2Dで定義されている楕円弧の開始角度と角度範囲である。
以上により t2 も求まる。交点PT2に関しても同様である。
|
intersectionPtsOfCircles
(static) |
private static CrossCurvePT[] intersectionPtsOfCircles(Segment2D segment1, Segment2D segment2)
引数, 戻り値はgetIntersectionPtsOfSegmentsと同じ。
円弧セグメント×円弧セグメントの交点計算。
|
intersectionPtsOfLineAndQuad
(static) |
protected static CrossCurvePT[] intersectionPtsOfLineAndQuad(Segment2D segment1, Segment2D segment2)
引数, 戻り値はgetIntersectionPtsOfSegmentsと同じ。
直線セグメント×2次曲線セグメントの交点計算。
|
intersectionPtsOfLineAndCubic
(static) |
protected static CrossCurvePT[] intersectionPtsOfLineAndCubic(Segment2D segment1, Segment2D segment2)
引数, 戻り値はgetIntersectionPtsOfSegmentsと同じ。
直線セグメント×三次曲線セグメントの交点計算。
|
intersectionPtsOfArbitraries
(static)
|
private static CrossCurvePT[] intersectionPtsOfArbitraries(Segment2D segment1, Segment2D segment2)
引数, 戻り値はgetIntersectionPtsOfSegmentsと同じ。
任意曲線セグメント間の交点計算。
曲線セグメント1, 2を分割して各々Boxで覆い、Boxが重なれば、曲線セグメントをさらに分割して、同じチェックを行うことによって交点の近似点を求める(multisectionForInterSectionメソッド)。
ある程度分割が進んだ段階で、NewtonRaphsonForInterSectionメソッドを呼んで収束計算を行い、精度良く交点を求める。
|
multisectionForInterSection
(static)
|
private static void multisectionForInterSection(int depth, int numSubDiv, double delta,
Segment2D segment1, double t1s, double t1e, Segment2D segment2, double t2s, double t2e, Vector vector))
引数:
depth - 再帰呼び出しの深さ
numSubDiv - 再分割数のMax
delta - segment1, segment2の幅と高さがこの値以下になると再分割を停止してリターン
segment1 - 曲線セグメント1
t1s, t1e - Boxの交差チェックを行うsegment1の曲線パラメータ区間
segment2 - 曲線セグメント2
t2s, t2e - Boxの交差チェックを行うsegment2の曲線パラメータ区間
vector - 再分割を繰り返し、Boxどうしが交差している区間を格納して返す。
処理:
⋅ このメソッドの再帰呼び出しで処理をする。
⋅ 区間の分割は多分法で、segment1、segment2を最大でnumSubDiv分割する。
⋅ segment1、segment2の分割区間を覆うBoxの幅と高さがdelta(現在1ピクセル)以下になったら、分割を停止し引数のvectorに分割区間を格納してリターン。
|
boxCheck
(static)
|
private static boolean boxCheck(Rectangle2D box1, Rectangle2D box2)
box1とbox2は交差しているときにtrueを返す。
|
NewtonRaphsonFor
InterSection
(static)
|
private static CrossCurvePT NewtonRaphsonForInterSection(Segment2D segment1, double t1s, Segment2D segment2, double t2s)
引数:
t1s, t1e - segment1の交点が存在する可能性のある曲線パラメータ区間
t2s, t2e - segment2の交点が存在する可能性のある曲線パラメータ区間
戻り値: 交点オブジェクトCrosssCurvePTを返す。
収束判定:
⋅ 曲線パラメータの前回繰り返しとの差分量dt1, dt2が1e-12以下になったら収束と見なす。
エラー判定:
⋅ 繰り返し計算回数Max(現在10回)を超えたらエラー。
⋅ 2曲線の接ベクトルが平行になったらエラー。
⋅ 近似点の曲線パラメータt1, t2が[0,1]区間から外に出たらエラー。
|
 : Newton-Raphson法による交点計算
戻る=>任意2曲線間の交点 : Newton-Raphson法による交点計算
戻る=>任意2曲線間の交点
曲線パラメータをt1, t2 、曲線C1, C2のx,y成分を縦ベクトル表示で次のように表す(太文字はベクトル)。
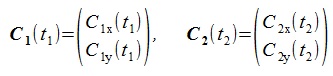
曲線C1, C2の交点は次の連立方程式の解である
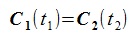
ここで
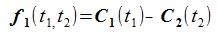
とおき、f(t1, t2)
の解をNewTon-Raphson法で求める。まずNewTon-Raphson法の近似式を求める。
dt1, dt2 を無限小とすれば、全微分、偏微分の関係により次式が成立している
(教科書ではdt1, dt2を普通∆ t1, ∆ t2と書く)。
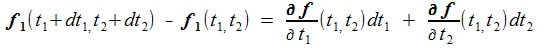
NewTon-Raphson法の近似式は、f(t1+ dt1 , t 2 + dt 2)=0と置いて求める。
ここで
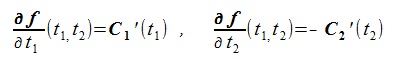
であるから、左辺と右辺を入れ替えて次式を得る。
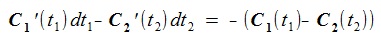
これを行列の形で書くと次式。
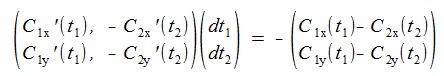
これからdt1, dt2 を求めt1+dt1->
t1, t2+dt2-> t2と置き換えて繰り返し計算を行う。
3.2 点から曲線上への投影点
戻る=>Curve2DUtil
メソッド
|
説明
|
getProjectionLines
(public)
|
public static CurvePT[] getProjectionLines(Point2D point, Vector2D dir, Curve2D curve)
処理:
point - 与えられた点。この点をdir方向に投影した曲線上の点を求める。
dir - 投影方向を表す Vector2Dオブジェクト。
curve - Curve2Dオブジェクト(パラメトリック曲線)
戻り値:
投影点のCurvePT オブジェクトの配列。投影点がないときは長さ0の配列を返す。
処理:
このメソッドが投影点計算のメインメソッドである。曲線セグメントごとに処理するため
getProjectionLineOnSegments メソッドを呼ぶ。投影点が複数求まった場合は、 eliminateDuplicationAndSort メソッドで重複チェックを行う。
下図は投影点計算の例である。マウス位置を0°, 45°, 90°,135°度方向に投影した
選択図形上の点を表示している。

|
eliminateDuplication
AndSort
(private)
|
private static CurvePT[] eliminateDuplicationAndSort(CurvePT[] PTs, double tolerance)
引数PTsで与えられるデータの重複チェックを行い、曲線パラメータが近い点を削除する。同時に曲線パラメータについてソートして出力する。
|
getProjectionLinesOnSegment
(private)
|
private static CurvePT[] getProjectionLinesOnSegment(Point2D point, Vector2D dir, Segment2D segment)
引数:
point - 与えられた点。この点をdir方向に投影した曲線セグメント上の点を求める。
dir - 投影方向を表す Vector2Dオブジェクト。
segment - Segment2D(曲線セグメント)オブジェクト。
戻り値:
投影点のCurvePT オブジェクトの配列。投影点がないときは長さ0の配列を返す。
処理:
曲線セグメントのタイプ(type)に応じて次のメソッドを呼ぶ。
⋅ タイプが LINE.
ProjectionToLine メソッドを呼ぶ。解析的計算で求める。
⋅ タイプが ARCでアフィン変換なし
ProjectionToCircularArc メソッドを呼ぶ。解析的計算で求める。
⋅ タイプが CUBIC、アフィン変換つきの ARC
ProjectionToArbitary メソッドを呼ぶ。収束計算で求める。
|
ProjectionToLine
(private)
|
private static CurvePT ProjectionToLine(Point2D point, Vector2D dir, Segment2D
segment)
引数:
point - 与えられた点。この点をdir方向に投影した曲線セグメント上の点を求める。
dir - 投影方向を表す Vector2Dオブジェクト。
segment - Segment2D(曲線セグメント)オブジェクト。
戻り値:
投影点のCurvePT オブジェクト。投影点がないときはnullを返す。
|
ProjectionToCircularArc
(private)
|
private static CurvePT[] ProjectionToCircularArc(Point2D pointt, Vector2D
dir, Segment2D segment)
引数:
point - 与えられた点。この点をdir方向に投影した曲線セグメント上の点を求める。
dir - 投影方向を表す Vector2Dオブジェクト。
segment - Segment2D(曲線セグメント)オブジェクト。
戻り値:
投影点のCurvePT オブジェクトの配列。投影点がないときは長さ0の配列を返す。
|
ProjectionToArbitrary
(private)
|
private static CurvePT[] ProjectionToArbitrary(Point2D pointt, Vector2D
dir, Segment2D segment)
引数:
point - 与えられた点。この点をdir方向に投影した曲線セグメント上の点を求める。
dir - 投影方向を表す Vector2Dオブジェクト。
segment - Segment2D(曲線セグメント)オブジェクト。
戻り値:
投影点のCurvePT オブジェクトの配列。投影点がないときは長さ0の配列を返す。
処理:
最初はパラメータ区間 (0≤t≤1) を分割して bisectionForProjectionLine を呼ぶ。
bisectionForProjectionLineメソッドから戻された区間に対して
NewtonRaphsonForProjectionLine
メソッドを呼んで高精度で投影点を求める。
|
bisectionFor
ProjectionLines
(private)
|
private static void bisectionForProjectionLine(Point2D point, Vector2D
dir, Segment2D segment, double ts, double te, Vector vector)
引数:
point - 与えられた点。この点をdir方向に投影した曲線セグメント上の点を求める。
dir - 投影方向を表す Vector2Dオブジェクト。
segment - Segment2D(曲線セグメント)オブジェクト。
ts,te - 曲線セグメントのパラメータ区間。この区間に投影点がある可能性があると、このメソッドを再帰呼び出しして、区間を細かくしてゆく。
vector - もし [ts,te] 区間が十分細かければ、vectorに登録してリターン。
|
NewtonRaphsonFor
ProjectionLines
(private)
|
private static CurvePT NewtonRaphsonForProjectionLines(Point2D point, Vector2D
dir, Segment2D segment, double ts, double te)
引数:
point - 与えられた点。この点をdir方向に投影した曲線セグメント上の点を求める。
dir - 投影方向を表す Vector2Dオブジェクト。
segment - Segment2D(曲線セグメント)オブジェクト。
ts,te - 曲線セグメントのパラメータ区間。
戻り値:
The CurvePT object. If there is no projected point, 戻り値 null.
処理:
収束判定:
⋅ |tn+1-tn|<epならば収束(eps=1.0e-12)。
エラーチェック:
⋅ 繰り返し回数が10回を超えたらエラーリターン。
⋅ 収束計算式の分母が0に近いとエラーリターン。
⋅ 近似解が[ts,te]外に出たらエラーリターン。
|
3.3 点から曲線への垂線
戻る=>Curve2DUtil
 計算式=>
NewtonRaphson法による垂線計算 計算式=>
NewtonRaphson法による垂線計算
メソッド
|
説明
|
getNormalLines
(public)
|
public static CurvePT[] getNormalLines(Point2D point, Curve2D curve)
引数:
point - 与えられた点
curve - Curve2D オブジェクト
戻り値:
pointからcurveへの垂線の足をCurvePT オブジェクトの配列を返す。垂線がないときは長さ0の配列を返す。
処理:
点から曲線への垂線を計算する最上位メソッド。
垂線がない時は長さ0の配列を返す。
曲線セグメントに分解して、下記のgetNormalLinesOnSegmentメソッドを呼ぶ。
処理の終了前に次のeliminateDuplicationAndSortを呼んで、出力データCurvePT[]の重複チェックとソートを行う。ソートはCurvePTのcurve曲線パラメータの小さい順。
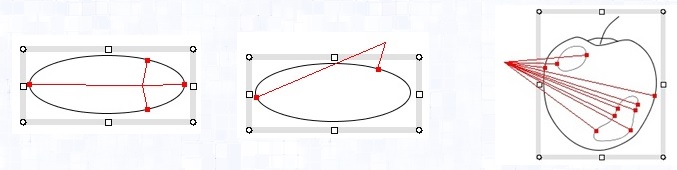
|
getNormalLinesOnSegment
(private)
|
private static CurvePT[] getNormalLinesOnSegment(Point2D point, Segment2D
segment)
点から曲線セグメントへの垂線を計算する。曲線セグメントが①直線、②円弧、③楕円弧(java.awt.geom.Arc2D), ④三次曲線、の4通りに分類。①, ②は初等計算式で解ける。③は垂線が一般には4本になるので解けない。④は一般には無理。
以上のことから①, ②は初等計算式で解き、③, ④にはNewton-Raphson法を使う。
|
NormalToLine
(private)
|
private static CurvePT NormalToLine(Point2D point, Segment2D segment)
点から直線セグメントへの垂線を計算し、その直線上の点を返す。垂線の端点が直線セグメントの外に出る時はnullを返す。
|
NormalToCircularArc
(private)
|
private static CurvePT[] NormalToCircularArc(Point2D point, Segment2D segment)
点から円弧セグメントへの垂線を計算し、円弧上の点を返す。垂線の端点が円弧セグメントの外に出る時はnullを返す。
|
NormalToArbitrary
(private)
|
private static CurvePT[] NormalToArbitrary(Point2D point, Segment2D segment)
点から任意曲線セグメントへの垂線を計算し、垂線の曲線セグメントの点を返す。
2分法bisectionForNormalLinesメソッドで近似点を計算し、NewtonRaphsonForNormalLinesメソッドで精度良く計算する。
最初にbisectionForNormalLinesを呼ぶ時は、曲線セグメントを細かく分割(現在128分割)して渡す。これは閉じた楕円など、接線方向が360度変わる図形に対処するためである。
|
bisectionForNormalLines
(private)
|
private static void bisectionForNormalLines(Point2D point, Segment2D segment,
double ts, double te, Vector vector)
引数
point - 与えられた点
segment - Segment2D(曲線セグメント)オブジェクト。
ts, te - segmentの曲線パラメータ区間
vector - 再分割を繰り返し、垂線が存在する可能性のある区間を格納して返す。
処理:
2分法により垂線の曲線上の点を求める。
⋅ このメソッドの再帰呼び出しで処理をする。
⋅ 区間の分割は2分法で行う。
⋅ segmentの両端の距離が一定以下(現在2ピクセル)以下になったら、分割を停止し引数のvectorに分割区間を格納してリターン。
|
NewtonRaphsonFor
NormalLines
(private)
|
private static CurvePT NewtonRaphsonForNormalLines(Point2D point, Segment2D
segment, double ts, double te)
引数:
point - 与えられた点
segment - Segment2D(曲線セグメント)オブジェクト。
⋅ts, te - segmentの曲線セグメントパラメータ区間
戻り値: 垂線の曲線上の点をCurvePTオブジェクトで返す
収束判定:
⋅ 曲線パラメータの前回繰り返しとの差分量dtが1e-10以下になったら収束と見なす。
エラー判定:
⋅ 繰り返し計算回数Max(現在20回)を超えたらエラー。
⋅ Newton-Raphsonの計算式が成立しない場合エラー。
⋅ 近似点の曲線パラメータtが[ts, te]区間から外に出たらエラー。
|
 : Newton-Raphson法による垂線計算
戻る=>点から曲線への垂線 : Newton-Raphson法による垂線計算
戻る=>点から曲線への垂線
次のようにf(t)を定める。
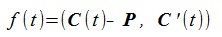 (a,b)は内積、C'(t)は曲線の微分
(a,b)は内積、C'(t)は曲線の微分
f(t)=0を満たすt を求めれば
C(t) が垂線の曲線上の点である。
dt を無限小とすれば次式が成立。
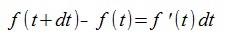
この式でf(t+dt)=0と置いた式がNewTon-Raphson法の繰り返し計算の式となる。
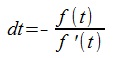
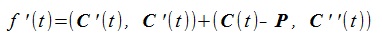
これからdt を求め、t+dt->t と置き換えて繰り返し計算を行う。
3.4 点から曲線への最短垂線
戻る=>Curve2DUtil
3.5 点から曲線への最短線
戻る=>Curve2DUtil
3.6任意2曲線間の共通垂線
戻る=>Curve2DUtil
 =>
処理方式 =>
処理方式
メソッド
|
説明
|
getNormalLinesBetweenShapes
(static)
|
public static Vector getNormalLinesBetweenShapes(Curve2D curve1, Curve2D curve2,
String shapeId1, String shapeId2)
引数:
curve1 - 第1 Curve2D オブジェクト。
curve2 - 第2 Curve2D オブジェクト。
shapeId1 - 輪郭線をcurve1とするShapeContainerのshapeId。
shapeId2 - 輪郭線をcurve2とするShapeContainerのshapeId。
戻り値:
curve1、curve2間の共通垂線および交点をNormalsInfoオブジェクトに設定し、Vectorに格納して返す。
処理:
曲線セグメントの組み合わせに分解して、下記 segmentsNormalLinesBetweenLines,
segmentsNormalLinesBetweenCircles
またはsegmentsNormalLinesBetweenArbitrariesメソッドを呼ぶ。
処理の終了前に、つぎのeliminateNormalLinesDuplicationメソッドを呼んで、
出力データであるNormalsInfoオブジェクトの重複チェックを行う。

 :曲線間の共通垂線を最上位メソッド。交点も求められる :曲線間の共通垂線を最上位メソッド。交点も求められる
|
eliminateNormalLinesDuplication
(static)
|
protected static Vector eliminateNormalLinesDuplication(Vector normalsVector)
引数normalsVectorに格納されたNormalsInfoオブジェクトの重複チェックを行う。
|
segmentsNormalLinesBetweenLines
(static)
|
protected static Vector segmentsNormalLinesBetweenLines(Segment2D segment1, Segment2D segment2)
引数:
segment1 - Segment2Dオブジェクト
segment2 - Segment2Dオブジェクト
戻り値:
Vector - NormalsInfoオブジェクトを格納して返す。
処理:
直線セグメント×直線セグメントの共通垂線計算。
∙ 共通垂線計算: 2つの直線セグメントが平行な場合にのみ共通垂線が存在する。
2つの直線セグメントが平行でない場合はリターン。
平行な場合は、直線セグメントの両端点からCurve2DUtil.ProjectionToLine
によって垂線の足を求め、2つの直線セグメントの共通垂線が存在する区間を求める。
出力するNormalsInfoにはtype=SegmentIntervalSolution
を設定する。
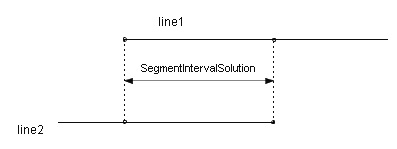
矢印の範囲に共通垂線が存在する
∙ 交点計算: Curve2DUtil.intersectionPtOfLinesで交点計算し、
NormalsInfoに値を設定してリターン。
NormalsInfoにはtype=SegmentSolutionを設定する。
|
segmentsNormalLinesBetweenCircles
(static) |
protected static Vector segmentsNormalLinesBetweenCircles(Segment2D segment1, Segment2D segment2)
引数:
segment1 - Segment2Dオブジェクト
segment2 - Segment2Dオブジェクト
戻り値:
Vector - NormalsInfoオブジェクトを格納して返す。
処理:
円弧セグメント×円弧セグメントの共通垂線計算。
∙ 共通垂線計算(1): 2つの円弧セグメントの中心点が一致するとき。
この場合、一方の円弧セグメントの両端点から、相手セグメントへの垂線の足を求め、
2つの円弧セグメントの共通垂線が存在する区間を求める。
出力するNormalsInfoにはtype=SegmentIntervalSolution
を設定する。
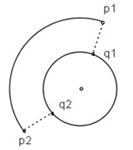
p1-p2区間、q1-q2区間に共通垂線が存在する。
∙ 共通垂線計算(2): 2つの円弧セグメントの中心点が一致しないとき。
この場合、2つの円弧セグメントの中心点を結ぶ直線を円弧上まで延長した直線が共通垂線になる
(Java Drawing Test Codes Figure 3.3)。
円弧ではなく両方とも完全円の場合、共通垂線は4本見つかる。
出力するNormalsInfoにはtype=SegmentSolution
を設定する。
∙ 交点計算: Curve2DUtil.intersectionPtsOfCirclesで交点計算し、
NormalsInfoに値を設定してリターン。
NormalsInfoにはtype=SegmentSolutionを設定する。
|
segmentsNormalLinesBetweenArbitraries
(static)
|
protected static Vector segmentsNormalLinesBetweenArbitraries(Segment2D segment1, Segment2D segment2)
引数:
segment1 - Segment2Dオブジェクト
segment2 - Segment2Dオブジェクト
戻り値:
Vector - NormalsInfoオブジェクトを格納して返す。
処理:
任意曲線セグメント間の共通垂線計算。
曲線セグメント1, 2を分割して
次のroughCheckメソッドで下記
処理方式の
ステップ1を実行して共通垂線のある区間を求める。
分割が十分細かくなると、NewtonRaphsonForNormalLinesBetweenShapes
メソッドを呼んで収束計算を行い、精度良く共通垂線を求める。
|
roughCheck
(static)
|
protected static void roughCheck(int depth, double stopSize, int[] numDiv,
Segment2D segments[], double[] T, Vector normalsVector)
引数:
depth - 再帰呼び出しの深さ。
stopSize - 再帰呼び出しを停止する曲線セグメントの分割サイズ。
分割サイズは曲線セグメントの分割区間を被覆するBoundingBoxのサイズのことである。
numDiv - 曲線セグメントの分割数。
numDiv[0]は曲線セグメント1、numDiv[1]は曲線セグメント2の分割数。
segments - 曲線セグメント1, 2を格納。
segments[0]は曲線セグメント1、segments[1]は曲線セグメント2。
T - 曲線セグメント分割区間を表す曲線パラメータ。
T[0]、T[1]は曲線セグメント1、T[2]、T[3]は曲線セグメント2の分割区間。
normalsVector - 共通垂線が存在する可能性のある区間をNormalsInfoに格納して返す。
NormalsInfoにはtype=SegmentHitIntervalを設定する。
処理:
 =>
処理方式
2.1 処理ステップ, 2.2 計算式,
図2.1, 2.2, 図2.3 =>
処理方式
2.1 処理ステップ, 2.2 計算式,
図2.1, 2.2, 図2.3
∙ このメソッドは再帰呼び出しで処理をする。
∙ 次のsegmentHitメソッドで曲線セグメント1, 2間に共通垂線が存在する可能性をテスト。
存在する可能性があれば、NormalsInfoオブジェクトをtype=SegmentHitIntervalで作成して、
normalsVectorに格納し、再帰的にこのroughCheckメソッドを呼ぶ。このときdepth引数には、depth+1をセットする。
∙ 区間の分割は2分法で、曲線セグメント1, 2の分割区間を覆うBoxの幅と高さが引数のstopSize以下になったら、
分割を停止し引数のnormalsVectorに分割区間をNormalsInfo
オブジェクト形式で格納してリターン。
|
segmentHit
(static)
|
protected static boolean segmentHit(Segment2D segment1, Segment2D segment2, double[] newT)
引数:
segment1 - 曲線セグメント1
segment2 - 曲線セグメント2
newT - 曲線セグメント分割区間を表すの曲線パラメータ。
newT[0]、newT[1]は曲線セグメント1、newT[2]、newT[3]は曲線セグメント2の分割区間。
戻り値:
boolean - 曲線セグメント1, 2が共通垂線を持つ可能性があるときtrueを返す。
処理:
次のrectHitメソッドにより判定を行う。
|
rectHit
(static)
|
protected static boolean rectHit(Point2D p1, Point2D p2, Vector2D e1, Vector2D e2, Rectangle2D rect)
引数:
p1 - 分割区間の端点。
p2 - 分割区間の端点。
e1 - p1での単位垂線ベクトル。
e2 - p2での単位垂線ベクトル。
rect - テストされる矩形。
戻り値:
int - rectがRegion AまたはBと共有部分を持つときtrueを返す。
処理:
引数rectの4頂点に対しptPositionで判定を行う。4頂点のうち少なくとも1点がRegion AまたはRegion Bに属すれば、
戻り値をtrueで返す。また4頂点のうちRegion CとRegion Dに属する点があれば、同様に戻り値をtrueで返す。
 =>
Java Drawing Test Codes, 2曲線への共通垂線の計算, 図3.1(c)。 =>
Java Drawing Test Codes, 2曲線への共通垂線の計算, 図3.1(c)。
|
ptPosition
(static)
|
public static int ptPosition(Point2D p1, Point2D p2, Vector2D e1, Vector2D e2, Point2D p)
引数:
p1 - 分割区間の端点。
p2 - 分割区間の端点。
e1 - p1での単位垂線ベクトル。
e2 - p2での単位垂線ベクトル。
p - この点がどの領域に属するかを判定する。
戻り値:
int - pが属する領域(Region A/B/C/D=1/2/3/4)
処理:
 =>
2.1 処理ステップ 図2.1, 2.2, 図2.3 =>
2.1 処理ステップ 図2.1, 2.2, 図2.3
|
NewtonRaphsonForNormalLinesBetweenShapes
(static)
|
protected static NormalsInfo NewtonRaphsonForNormalLinesBetweenShapes(Segment2D segment1, Segment2D segment2,
double t1s, double t2s)
引数:
segment1 - 曲線セグメント1
segment2 - 曲線セグメント2
t1s, t1e - segment1の共通垂線が存在する可能性のある曲線パラメータ区間
t2s, t2e - segment2の共通垂線が存在する可能性のある曲線パラメータ区間
戻り値:
共通垂線が存在する可能性のある曲線パラメータをNormalsInfoオブジェクトに設定して返す。
NormalsInfoオブジェクトのタイプはtype=SegmentSolutionである。
収束判定:
⋅ 曲線パラメータの前回繰り返しとの差分量dt1, dt2が1e-12以下になったら収束と見なす、など。
エラー判定:
⋅ 繰り返し計算回数Max(現在10回)を超えたらエラー。
⋅ 近似点の曲線パラメータt1, t2が[0,1]区間から外に出たらエラー。
など。
|
 :
処理方式
戻る=>任意2曲線間の共通垂線 :
処理方式
戻る=>任意2曲線間の共通垂線
1. 関連事項
単体テスト, 結果 =>
Java Drawing Test Codes: 2曲線への共通垂線の計算: このドキュメントはテスト結果を含む。
2. 処理方法
戻る=>任意2曲線間の共通垂線
2.1 処理ステップ(図2.1, 2.2)
ステップ1. 共通垂線の存在可能性の判定
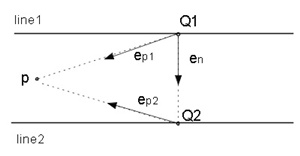
図2.1に示すように曲線curve1を細かく分割して、分割区間に変曲点(inflection point)を持たないようにする。
分割区間の両端p1、p2でcurve1の垂線line1, line2を作成する。
一方、曲線curve2も細かく分割し、分割区間を矩形で覆う(被覆矩形: bounding box)。
このとき、curve2の被覆矩形の一部または全部が、line1, line2に挟まれた領域(水色の領域)内にあれば、
その被覆矩形内部のcurve2分割区間と、curve1の分割区間(p1, p2区間)には共通垂線が存在する可能性があると判定できる。
またこのようにして見つけたcurve2の分割区間に対して垂線line1, line2を作成し、
curve1の分割区間を被覆矩形で覆って、前記と同様な判定処理を行い、
共通垂線があり得ると判定されれば、共通垂線の存在可能性はより高くなる(図3.2)。
ステップ2. 二分法による高精度化
ステップ1の方法で共通垂線があり得ると判定されたcurve1, curve2の分割区間を、2分法で分割し、
ステップ1と同様な判定処理を行い、共通垂線の存在する分割区間の範囲を狭める。
この処理は分割区間が十分に小さくなるまで、再帰呼び出しで処理する。
ステップ3. Newton Raphson法による高精度計算
ステップ2で十分に小さくなった分割区間の中央点を初期値としてNewton Raphson法を実行する。
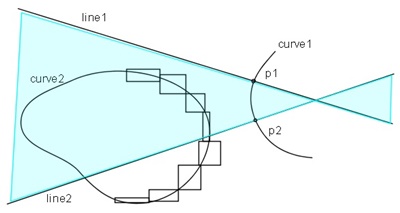 |
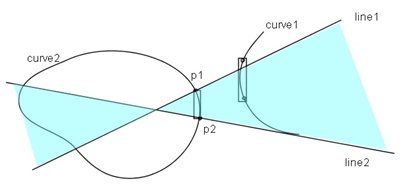 |
| 図 2.1 共通垂線の存在可能性の判定(1) |
図 2.2 共通垂線の存在可能性の判定(2) |
2.2 計算式
戻る=>任意2曲線間の共通垂線
2.2.1 上記Step1の計算式
(図2.3(a)-(e))
被覆矩形の一部または全体が2直線(line1, line2)に挟まれた領域にあるか否かを判定するには、
被覆矩形の頂点が、その領域にあるか否かを判定できれば良い。
下記(a)-(d)は、line1, line2が並行でない場合、(e)は平行な場合について述べる。
図2.3(a)に示すように。line1, line2方向の単位ベクトルをe1, e2 とし、line1, line2の
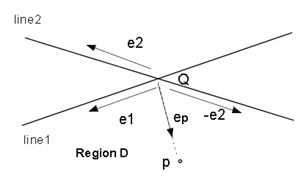
交点Qからpへ向かう単位ベクトルをep とする。点pが領域A(Region A)に存在するための条件を求める。
e1, e2 , ep は2次元ベクトルであるが三次元ベクトルと見なし、
ベクトルの外積のz値を2次元ベクトルの外積値(スカラー)として扱う。
e1×e2 =e1x * e2y - e1y * e2x(1)
e1×e2 はe1とe2 が作る平行四辺形の符号つき面積である。
ここではe1×e2 ≧0と仮定する(e1×e2<0ならばe11とe2 を交換する)。
(a) pが領域Aにあるための条件はつぎの式が成立することである(図2.3(a))
0≦e1×ep ≦e1×e2 かつ0≦ep×e2 ≦e1×e2(2)
(b)pが領域Bにあるための条件(図2.3(b))
0≦(-e1)×ep≦(-e1)×(-e2) かつ0≦ep×(-e2)≦(-e1)×(-e2)
=> -(e1×e2)≦e1×ep≦0 かつ-(e1×e2)≦ep×e2≦0(3)
(c) pが領域Cにあるための条件(図3.3(c))
0≦ep×(-e1)≦e2×(-e1)かつ0≦e2×ep≦e2×(-e1)
=> 0≦e1×ep≦e1×e2かつ0≦-(ep×e2)≦e1×e2
=> 0≦e1×ep≦e1×e2 かつ-(e1×e2)≦ep×e2≦0(4)
(d) pが領域Dにあるための条件(図2.3(d))
0≦ep×e1≦(-e2)×e1かつ0≦(-e2)×ep≦(-e2)×e1
=> 0≦-(e1×ep)≦e1×e2かつ0≦ep×e2≦e1×e2
=> -(e1×e2)≦e1×ep≦0 かつ0 ≦ep×e2≦e1×e2(5)
(e) pがline1, line2の間の領域あるための条件(図2.3(e))
図2.3(e)にあるように単位ベクトルを定義すると、条件はつぎ。
0≦en×ep1≦|Q2-Q1| (6)
ここで|Q2-Q1|はline1, line2間の距離。
(注)実際のテスト結果を下のJava Drawing Test Codes 図3.1, 3.2に示す。
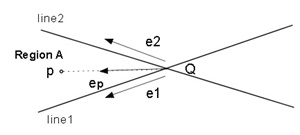
(a) |
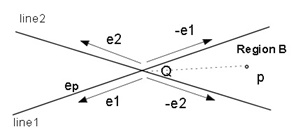
(b) |
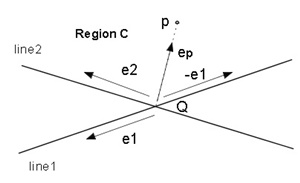
(c) |
(d) |
(e) |
|
| 図 2.3 ステップ1の計算式 |
2.2.2 上記ステップ3のNewton Raphson法の計算式戻る=>page top
曲線パラメータをt1, t2、曲線C1, C2のx,y成分を縦ベクトル表示で次のように表す(太文字はベクトル)。
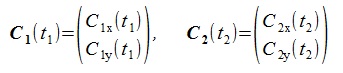 (1) (1)
共通垂線を求めるには、2曲線間の距離(次式)をローカルに最小化(Local Minimum)にするt1, t2を求めればよい。
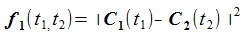 (2) (2)
最小化するには次の条件が必要である(はベクトルの内積)。
 (3) (3)
上式の右辺をf1(t1,t2), f2(t1,t2) と書く。
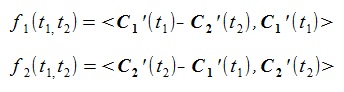 (4) (4)
dt1, dt2 を無限小とすれば(教科書ではΔt1, Δt2 と書く),
f1(t1,t2), f2(t1,t2)
に対しては全微分、偏微分の関係から次式が成立。
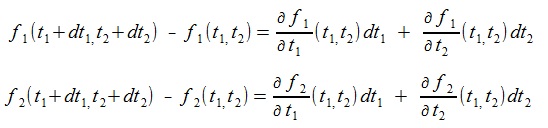 (5) (5)
ここで、(5)式右辺の偏微分は次式で与えられる。
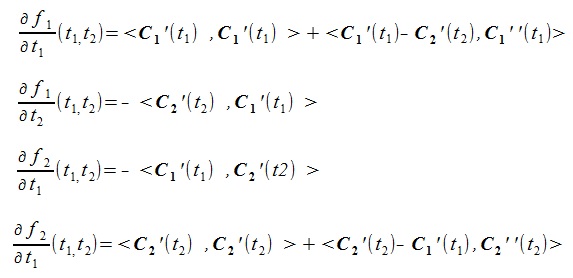 (6) (6)
NewTon-Raphson法の近似式は、次のように(5)式の左辺の項を0と置いて求める。
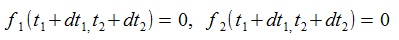 (7) (7)
(5)式は次のようになる。
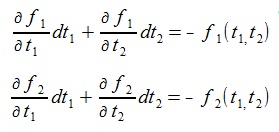 (8) (8)
(8)式マトリックを使い、次のように書ける。
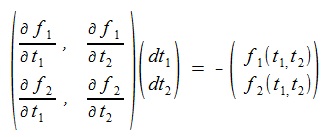 (9) (9)
これを解けば、dt1, dt2 は次のように求まる(detはdeterminant)
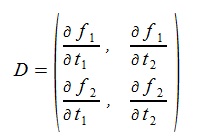 (10) (10)
ここでDは次のマトリックス。
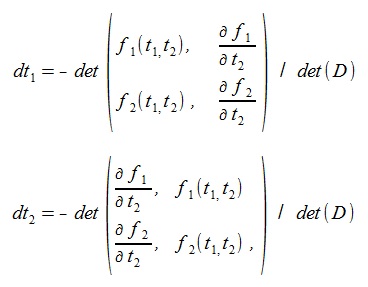 (11) (11)
3.7 任意2曲線間の最短線
戻る=>Curve2DUtil
3.8 曲線の方向反転
戻る=>Curve2DUtil
メソッド
|
説明
|
reverseCurve2D
(public) |
public static Curve2D reverseCurve2D(Curve2D curve)
引数:
curve - Curve2D オブジェクト
戻り値:
方向を反転した曲線をCurve2Dオブジェクトで返す。
|
3.9 曲線の切断
戻る=>Curve2DUtil
メソッド
|
説明
|
trimCurve2D
(public)
|
public static Curve2D trimCurve2D(Curve2D curve, double t1, double t2)
引数:
curve - Curve2D オブジェクト
t1,t2 - 切断する区間
戻り値:
切断された曲線をCurve2Dオブジェクトで返す。
処理:
閉じていない曲線の場合は必ずt1<t2で呼び出すこと。閉曲線でt1>t2の時は、[t1,te] 区間と[ts,t2}区間を一本につないで返す。
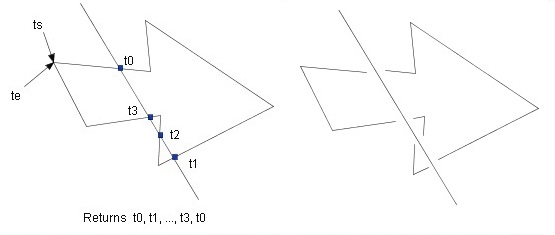
下図左において、矢印状のポリゴンは直線セグメント7本から構成されるので、ts=0.0<t0<t1<t2<t3<te=7.0。
切断区間は[t0,t1], [t1,t2], [t2,t3], [t3,t0]で4本の折れ線が作成される。
右図は結果で、見易いように4本の折れ線を少しづつずらして表示している。
|
3.10 曲線を単純な形式に変換
戻る=>Curve2DUtil
メソッド
|
説明
|
getSimpleCurve2D
(public) |
public static Curve2D getSimpleCurve2D(Curve2D curve)
引数:
curve - Curve2D オブジェクト
戻り値:
単純化された曲線をCurve2Dオブジェクトで返す。
処理:
より簡単な形式のパラメトリック曲線に変換して返す。たとえば曲線セグメントが全て直線で構成されているときは、Line2DEまたはPolyline2DEを返すなど。
このメソッドは曲線の接続(ConnectCurves)などで、接続曲線をGeneralCurve2D形式で作成するが、より簡単な形式で表せるときに使う。
|
3.11 曲線セグメントをまとめる
戻る=>Curve2DUtil
メソッド
|
説明
|
arrangeCurveSegment
(public) |
public static Curve2D arrangeCurveSegment(Curve2D curve)
引数:
curve - Curve2D オブジェクト
戻り値:
処理済みのCurve2Dオブジェクトを返す。
曲線セグメントがまとまらなかった場合引数のコピー(clone)を返す。
処理:
curveの連続する曲線のセグメント(Segment2D)が
一本に結合できる場合、それらを結合して一本にまとめる。
例えば、同じ方向の直線セグメントが2本続く時、一本にまとめるなど。
現実には楕円(円)を直線で分割(CutShape)すると、
楕円の始終点を含む部分は、2個の孤(Arc2D)から構成されるが、これらは一本にまとめられる。
|
uniteSegment2Ds
(private) |
private static Segment2D uniteSegment2Ds(Segment2D segment1, Segment2D segment2)
引数:
segment1 - Segment2Dオブジェクト
segment2 - Segment2Dオブジェクト
戻り値:
segment1とsegment2が1本に接続されたとき、そのセグメントを返す。1本に接続されなかった時、nullを返す。
処理:
arrangeCurveSegmentから呼ばれる。segment1とsegment2がともに直線(Line2D)または孤(Arc2D)の場合だけ処理する。
segment1とsegment2がともにQubicCurve2Dであっても何もしない。
|
3.12 延長量を指定して曲線を延長
戻る=>Curve2DUtil
メソッド
|
説明
|
extendCurve2D
(public) |
public static Curve2D extendCurve2D(Curve2D curve, double extension, int
pos)
引数:
curve - Curve2D オブジェクト
extension - 延長量
pos - 0: 始点側を延長. 1: 終点側を延長
戻り値:
延長されたCurve2D オブジェクトを返す。
処理:
曲線を延長する。始点側を延長するときはreverseCurve2Dを呼んで曲線を反転してからextendSegment2Dを呼ぶ。
|
extendSegment2D
(private) |
private static Segment2D extendSegment2D(Segment2D segment, double extension)
引数:
segment - Segment2Dオブジェクト
extension - 延長量
戻り値:
segmentがLine2D/Arc2Dセグメントのとき:segmentの終点側を延長して返す。
segmentがCubicCurve2Dセグメントのとき:segmentの終点の接線方向に延長したCubicCurve2セグメントを返す。
処理:
extendCurve2Dから呼ばれる。必ずsegmentの終点側を延長するので、extendCurve2Dで始点側を延長するときはreverseCurve2Dで方向を反転してから、このメソッドを呼ぶ。
|
3.13 曲線の始点、終点を指定して曲線の延長
戻る=>Curve2DUtil
メソッド
|
説明
|
extendCurve2DByPT
(public) |
public static Curve2D extendCurve2DByPT(Curve2D curve, Point2D PT)
引数:
curve - Curve2D オブジェクト
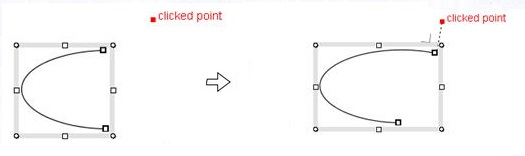
PT - PTに近い側を延長する。下図のようにclicked point(PT)から延長曲線への垂線の位置が終点となる位置まで延長する。
戻り値:
延長されたCurve2D オブジェクトを返す。
処理:
曲線を延長する。始点側を延長するときはreverseCurve2Dを呼んで曲線を反転してからextendSegment2DByPTを呼ぶ。
|
extendSegment2DByPT
(private) |
private static Segment2D extendSegment2DByPT(Segment2D segment, Point2D
PT)
引数:
segment - Segment2Dオブジェクト
PT - extendCurve2DByPTと同じ。
戻り値:
segmentがLine2D/Arc2Dセグメントのとき:segmentの終点側を延長して返す。
segmentがCubicCurve2Dセグメントのとき:segmentの終点の接線方向に延長したCubicCurve2セグメントを返す。
|
3.14 3点から円弧を作成
戻る=>Curve2DUtil
メソッド
|
説明
|
createCircularArcs
(public)
|
private static Arc2D[] createCircularArcs(Point2D p1, Vector2D tangent1,
Point2D p2, Vector2D tangent2)
引数:
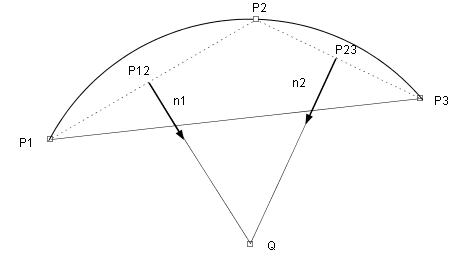
p1,p2,p3 - 円弧の始点、通過点、終点
戻り値:
p1,p2を端点とする円弧とp2,p3を端点とする円弧を返す。
p1,p2,p3が同一直線上にあるときは、長さ0の配列を返す。
処理:
getCrossPointを使えば円弧の中心点Qが求まる。またQ、p1、p2から円弧の中心角も求まる。
第1の円弧はp1を端点としQとp2を結ぶ直線上にもうひとつの端点を持つ円弧、
第1の円弧はQとp1を結ぶ直線上に端点を持ち, p2をもうひとつの端点とする円弧である。
|
getCrossPoint
(private)
|
private static Point2D getCrossPoint(Vector2D p1, Vector2D n1, Vector2D
p2, Vector2D n2)
createCircularArcsメソッドから呼ばれる。p1を通りn1方向の直線とp2を通りn2方向の直線との交点を返す。
|
3.15 distanceBetweenBoxes
戻る=>Curve2DUtil
メソッド
|
説明
|
distanceBetweenBoxes
(private)
|
public static double distanceBetweenBoxes(Rectangle2D box1, Rectangle2D box2)
box1とbox2の距離を返す。box1とbox2が重なっているときは距離0。
|
3.16 getMaxBox
戻る=>Curve2DUtil
メソッド
|
説明
|
getMaxBox
(private)
|
public static Rectangle2D getMaxBox(Rectangle2D[] boxes)
配列で与えられるboxesを全て覆う最小のRectangle2Dを返す。
|
3.17 NormalsInfoサブクラス
戻る=>Curve2DUtil
public static class NormalsInfo
フィールド
|
説明
|
type
|
public int type = 0;
次の定数 Solution - SegmentHitInterval のいずれかの値を設定する。
|
Solution
|
public final static int Solution = 0;
このオブジェクトがgetNormalLinesBetweenShapesメソッド
で求まる解を格納するときに、この値をtypeに設定する。
|
IntervalSolution
|
public final static int IntervalSolution = 1;
getNormalLinesBetweenShapesメソッドで求まる解が範囲で求まるときに、この値をtypeに設定する。
対象図形(引数 curve1, curve2)が
直線と直線、円弧と円弧などの場合に解は範囲で求まるケースがある。
curve1, curve2はCurve2D抽象クラスのオブジェクトである。
|
SegmentPtSolution
|
public final static int SegmentPtSolution = 2;
現在、使われていない。
|
SegmentSolution
|
public final static int SegmentSolution = 3;
曲線セグメント間の共通垂線の解を格納するときに、この値をtypeに設定する。
共通垂線を求めるメソッドは、
segmentsNormalLinesBetweenLines,
segmentsNormalLinesBetweenCircles,
segmentsNormalLinesBetweenArbitrariesである。
|
SegmentIntervalSolution
|
public final static int SegmentIntervalSolution = 4;
曲線セグメント間の共通垂線の解が範囲のとき、この値をtypeに設定する。
共通垂線を求めるメソッドは、上記と同様である。
|
SegmentHitInterval
|
public final static int SegmentHitInterval = 5;
roughCheckメソッドの出力NormalsInfoオブジェクトのtypeに設定する。
|
TypeString
|
public final String[] TypeString
= {"Solution", "IntervalSolution","SegmentPtSolution","SegmentSolution",
"SegmentIntervalSolution ", "SegmentHitInterval"};
typeの文字列表現。
|
shapeIds
|
public String[] shapeIds=new String[2];
getNormalLinesBetweenShapesメソッドの引数 curve1, curve2を
それぞれ所有するShapeContainerの名称
(shapeId)を設定する。
curve1, curve2はCurve2D抽象クラスのオブジェクトである。
|
curves
|
public Curve2D[] curves = new Curve2D[2];
getNormalLinesBetweenShapesメソッドの引数 curve1, curve2
のオブジェクトを設定する。
curve1, curve2はCurve2D抽象クラスのオブジェクトである。
|
t
|
public double[] t = new double[2];
type=Solution,
SegmentSolutionの場合に値を設定する。
共通垂線の両端点のcurve1, curve2上の曲線パラメータt1, t2を格納する。
curve1, curve2は上記curvesのcurves[0], curves[1]に対応し、
Curve2D抽象クラスのオブジェクトである。
|
segments
|
public Segment2D[] segments = new Segment2D[2];
type=SegmentSolution,
SegmentIntervalSolution,
SegmentHitInterval
の場合に値を設定する。
curve1, curve2の曲線セグメント(Segment2D)を格納する。
|
depth
|
public int depth;
type=SegmentHitInterval
のときのみ設定する。
depthはroughCheck再帰呼び出しメソッドの引数として渡される。
再帰呼び出しが終了したときのdepth値をこのフィールドに設定する。デバッグおよび参考用のデータである。
|
numDiv
|
public int[] numDiv = new int[2];
type=SegmentHitInterval
のときのみ設定する。
numDivはroughCheck再帰呼び出しメソッドの引数として渡される。
上記depthと同様、再帰呼び出しが終了したときのdnumDiv値をこのフィールドに設定する。デバッグおよび参考用のデータである。
|
divId
|
public int[] divId = new int[2];
type=SegmentHitInterval
のときのみ設定する。
divIdはroughCheckメソッドで使われる変数で、
曲線セグメント(Segment2D)を分割したときの分割番号を記録する。
再帰呼び出しが終了したときのdivId値をこのフィールドに設定する。デバッグおよび参考用のデータである。
|
interval
|
public double[] interval = new double[4];
type=IntervalSolution,
SegmentIntervalSolution,
SegmentHitInterval
の場合に値を設定する。共通垂線がある範囲に存在するときに使う。
t1=interval[0], t2=interval[1]は, curvesのcurves[0]または
segmentsのsegments[0]の曲線パラメータの範囲を設定する。
同様にt3=interval[2], t4=interval[3]は, curvesのcurves[1]または
segmentsのsegments[1]の曲線パラメータの範囲を設定する。
|
boxSize
|
public double[] boxSize = new double[2];
type=SegmentHitInterval
の時のみ値を設定する。
segmentsのsegments[0], segments[1]を覆う矩形の幅、高さの大きい方の値を設定する。
デバッグおよび参考用のデータである。
|
メソッド
|
説明
|
コンストラクター1
|
public NormalsInfo(int type, String shapeId1, String shapeId2,
Curve2D curve1, Curve2D curve2, double t1, double t2)
type=Solution
のコンストラクター。
|
コンストラクター2
|
public NormalsInfo(int type, String shapeId1, String shapeId2,
Curve2D curve1, Curve2D curve2, double[] interval)
type=IntervalSolution
のコンストラクター。
|
コンストラクター3
|
public NormalsInfo(int type, Segment2D segment1, Segment2D segment2, double t1, double t2)
type=SegmentSolution
のコンストラクター。
|
コンストラクター4
|
public NormalsInfo(int type, Segment2D[] segments, double[] interval)
type=SegmentIntervalSolution
のコンストラクター。
|
コンストラクター5
|
public NormalsInfo(int type, Segment2D[] segments, int depth, int[] numDiv, int[] divId,
double[] interval, double[] boxSize)
type=SegmentHitInterval
のコンストラクター。
|
getTypeString
|
public String getTypeString()
フィールド変数type値を返す。
|
getBoxSize
|
public double[] getBoxSize()
フィールド変数boxSize値を返す。
|
getAngle
|
public double[] getAngle()
共通垂線とcurves[0], curves[1],
またはsegments[0], segments[1]のなす角度を計算して返す。
共通垂線が区間で存在するときは、区間の中央点で計算する。
90度ならば計算結果は正しい。デバッグおよび参考用である。
|
getDistance
|
public double getDistance()
共通垂線の長さを計算して返す。共通垂線が区間で存在するときは、区間の中央点で計算する。
|
toString
|
public String toString()
フオブジェクトの文字列表現を返す。
|
4. Vector2Dクラス
戻る=>page top
public class Vector2D
2次元ベクトル計算のライブラリ
|
フィールド
|
説明
|
double x
|
double x: ベクトルのx成分
|
double y
|
double : ベクトルのy成分
|
|
メソッド
|
説明
|
コンストラクタ
|
public Vector2D(double x, double y)
引数のx,y成分をフィールド変数に設定。
|
コンストラクタ
|
public Vector2D(Point2D point)
引数pointのx,y成分をフィールド変数に設定。
|
getX
|
public double getX():フィールド変数xを返す
|
getY
|
public double getY():フィールド変数yを返す
|
setX
|
public void setX(double x) :フィールド変数xに引数を設定
|
setY
|
public void setY(double y) :フィールド変数yに引数を設定
|
toString
|
public String toString():文字列表現を返す。
|
clone
|
public Object clone():クローンを返す。
|
add
(static)
|
public static Vector2D add(Vector2D vec1, Vector2D vec2)
vec1+vec2を返す
|
sub
(static)
|
public static Vector2D sub(Vector2D vec1, Vector2D vec2)
vec1-vec2を返す
|
sub
(static)
|
public static Vector2D sub(Point2D p1, Point2D p2)
p1-p2をVector2Dで返す。
|
multiply
(static)
|
public static Vector2D multiply(double scalar, Vector2D vec)
scalar*vecを返す。
|
mult
(static)
|
public static Vector2D mult(double scalar, Vector2D vec)
multiplyと同じ。メソッド名が違うだけ。
|
sproduct
(static)
|
public static double sproduct(Vector2D vec1, Vector2D vec2)
vec1、vec2のスカラープロダクト(内積)を返す。
|
vproduct
(static)
|
public static double vproduct(Vector2D vec1, Vector2D vec2)
vec1、vec2のベクトルプロダクト(外積)を返す。vec1、vec2を三次元ベクトルと見なしで外積を作ったときの第3軸値。
|
isSameDirection
(static)
|
public static boolean isSameDirection(Vector2D vec1, Vector2D vec2, double
tolerance)
vec1、vec2ベクトルの成す角度(単位はdegree)がtolerance以下ならばtrueを返す。
|
unitVector
(static)
|
public static Vector2D unitVector(Vector2D vec)
単位ベクトルを返す。長さが1e-12以下のベクトルの時は0ベクトルを返す。
|
normalVector
(static)
|
public static Vector2D normalVector(Vector2D vec)
vecに直交するベクトルを返す。
|
unitNormalVector
(static)
|
public static Vector2D unitNormalVector(Vector2D vec)
vecに直交する単位ベクトルを返す。
|
project
(static)
|
public static Vector2D project(Vector2D vec1, Vector2D vec2)
vec1の長さを持つvec2方向ベクトルを返す。
|
length
(static)
|
public static double length(Vector2D vec)
ベクトル長を返す。
|
dist
(static)
|
public static double dist(Vector2D vec1, Vector2D vec2)
vec2-vec1の長さを返す。
|
dist
(static)
|
public static double dist(Point2D p1, Point2D p2)
p2-p1の長さ(p1,p2の距離)を返す。
|
crossPoint
(static)
|
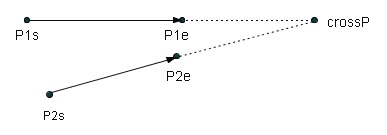
public static CrossCurvePT crossPoint(Point2D p1s, Point2D p1e, Point2D p2s, Point2D p2e)
点crossPをCrossCurvePTにセットして返す。
|
5. Matrix2Dクラス
戻る=>page top
public class Matrix2D

2次元マトリックスのライブラリ。java.awt.geom.AffineTransformの処理を一部含む。
|
フィールド
|
説明
|
|
matrix
|
double[][] matrix
3*3の配列。マトリックス要素をストアする。
|
|
メソッド
|
説明
|
コンストラクタ
|
public Matrix2D()
単位マトリックスオブジェクトを作成
|
コンストラクタ
|
public Matrix2D(double[] elm)
引数で指定された要素を持つマトリックスオブジェクトを作成。
elmは6個の配列で、m00, m10, m01, m11, m02, m12の順。
|
getElm
|
public double[][] getElm()
フィールド変数matrixを返す。
|
getElm
|
public double getElm(int i, int j)
フィールド変数matrixのi,j成分を返す。
|
setElm
|
public void setElm(int i, int j, double elm)
フィールド変数matrixのi,j成分に引数elmを設定。
|
addElm
|
public void addElm(int i, int j, double add)
フィールド変数matrixのi,j成分に引数addを加える。
|
getAffineTransform
|
public AffineTransform getAffineTransform()
このMatrix2Dオブジェクトからjava.awt.geom.AffineTransformを返す。
AffineTransformはマトリックスの1、2行目で決まり、要素の並びは、m00, m10, m01, m11, m02, m12の順である。
|
setAffineTransform
|
public void setAffineTransform(AffineTransform affine)
java.awt.geom.AffineTransformをMatrix2Dオブジェクトに設定する。
|
toString
|
public String toString():文字列表現を返す
|
transForm
(static)
|
public static Vector2D transForm(Matrix2D M, Vector2D vec)
vecをマトリックス変換した結果を返す。
|
transForm
(static)
|
public static Point2D transForm(Matrix2D M, Point2D p)
pをマトリックス変換した結果を返す。
|
scalarMult
(static)
|
public static Matrix2D scalarMult(double mult, Matrix2D M)
マトリックスMをスカラー倍した結果を返す。
|
multMatrix
(static)
|
public static Matrix2D multMatrix(Matrix2D M1, Matrix2D M2)
マトリックスM1, M2の積を返す。
|
InverseMatrix
(static)
|
public static Matrix2D InverseMatrix(Matrix2D M)
マトリックスMをの逆マトリックスを返す。Matrix.InverseMatrixを使う。
|
getScaleMatrix
(static)
|
public static Matrix2D getScaleMatrix(double scale)
scale倍のマトリックスを返す。m00=scale, m11=scale, m22=1で他の要素は0。
|
getResizeMatrix
(static)
|
public static Matrix2D getResizeMatrix(Rectangle2D oldBox, Rectangle2D
newBox)
oldBoxをnewBoxに変換する移動⋅ リサイズマトリックスを返す。
|
getRotationMatrix
(static)
|
public static Matrix2D getRotationMatrix(Point2D anchorP, Vector2D vec1,
Vector2D vec2)
anchorPを固定点とし、vec1をvec2へ長さも含めて一致させる回転マトリックスを返す。拡大/縮小を伴う。
|
getFlipMatrix
(static)
|
public static Matrix2D getFlipMatrix(int direction, double value)
鏡像変換のマトリックスを返す。
direction=0のとき水平方向の鏡像でvalueは鏡の位置のx座標。鏡はx軸に直交するように置かれる。
direction=1のとき垂直方向の鏡像でvalueは鏡の位置のy座標。鏡はy軸に直交するように置かれる。
|
multMatrix
(static)
|
public static AffineTransform multMatrix(AffineTransform M1, AffineTransform
M2)
AffineTransform M1,M2の積を返す。
|
print
(static)
|
public static void print(Matrix2D M)
マトリックスMをプリントする。
|
6. Matrixクラス
戻る=>page top
public class Matrix
一般の多次元マトリックスのライブラリ。
現在のところスプライン曲線作成に使っている。参照=>FergusonCurve2D.createNaturalSpline
|
フィールド
|
説明
|
eps
|
static double eps=1e-12
0判定に使う。
|
|
メソッド
|
説明
|
GaussianElimination
(static)
|
public static double[] GaussianElimination(double[][] A0, double[] b0)
A0*x=b0をガウス消去法で解きxを返す。処理が終了したときA0, b0は変更されない。
|
InverseMatrix
(static)
|
public static double[][] InverseMatrix(double[][] A)
ガウス消去法を使って逆マトリックスを返す。
|
multMatrix
(static)
|
public static double[][] multMatrix(double[][] A, double[][] B)
マトリックスM1, M2の積を返す。
|
print
(static)
|
public static void print(double[][] A, double[] b, double[] x)
A*x=b形式のA, b, xをプリントし、残差を表示する。
|
|
![]()
![]()
![]()
![]()
 計算式=>
NewtonRaphson法による交点計算方法
計算式=>
NewtonRaphson法による交点計算方法 : Newton-Raphson法による交点計算
戻る=>任意2曲線間の交点
: Newton-Raphson法による交点計算
戻る=>任意2曲線間の交点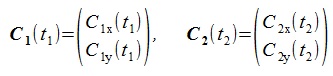
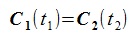
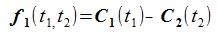
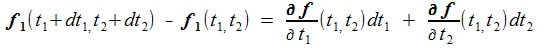
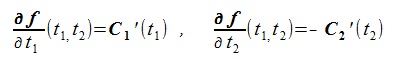
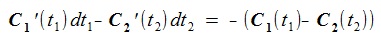
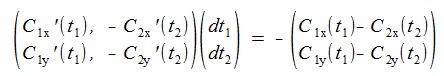
 計算式=>
NewtonRaphson法による垂線計算
計算式=>
NewtonRaphson法による垂線計算 : Newton-Raphson法による垂線計算
戻る=>点から曲線への垂線
: Newton-Raphson法による垂線計算
戻る=>点から曲線への垂線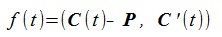 (a,b)は内積、C'(t)は曲線の微分
(a,b)は内積、C'(t)は曲線の微分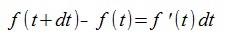
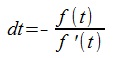
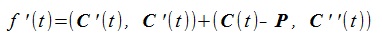
 =>
処理方式
=>
処理方式 :
処理方式
戻る=>任意2曲線間の共通垂線
:
処理方式
戻る=>任意2曲線間の共通垂線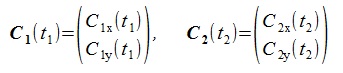 (1)
(1)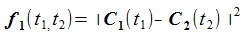 (2)
(2) (3)
(3)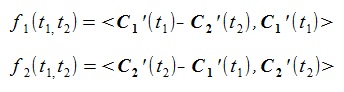 (4)
(4)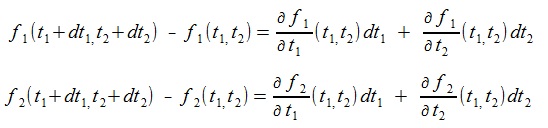 (5)
(5)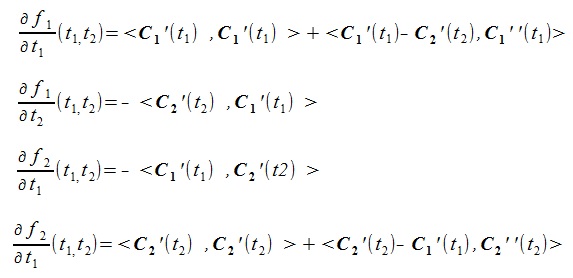 (6)
(6)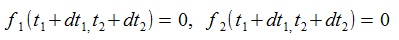 (7)
(7)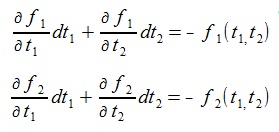 (8)
(8)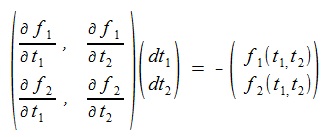 (9)
(9)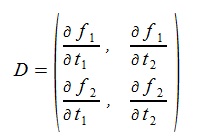 (10)
(10)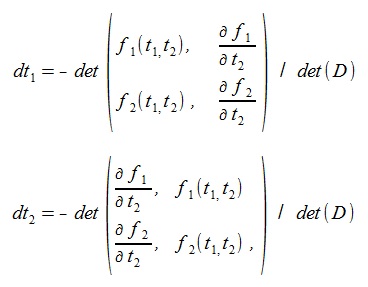 (11)
(11)