|
Summary:
The CrossCurvePT class
and the CurvePT class represents a point on a curve.
The Curve2DUtil class mainly provides the function of
calculating the intersection points between two curves and the function of
calculating the lines normal to a given curve which pass a given point.
The Vector2D class provides the operations for 2D vector.
The Matrix2D class provides the operations for 2D transform matrix.
The Matrix class provides the Gaussian elimination method to create a spline curve.
|
| Classes on this page:
CrossCurvePT, CurvePT,
Curve2DUtil,
Vector2D, Matrix2D, Matrix |
 =>
DrawTest: Intersection between two arbitrary curves ,
Normal lines to a arbitrary curve =>
DrawTest: Intersection between two arbitrary curves ,
Normal lines to a arbitrary curve
Common normal lines between two shapes
1. Class CrossCurvePT
return=>page top
public class CrossCurvePT
This class represents an intersection point of two curves. This object
has the parameters - t1, t2 - of the first curve and the second curve.
| Field |
Description |
t1
|
public double t1
The parameter of the first curve which represents the intersection point
of the two curves.
|
t2
|
public double t2
The parameter of the second curve which represents the intersection point
of the two curves
|
p1
|
Point2D p1
The intersection point on the first curve.
|
p2
|
Point2D p2
The intersection point on the second curve.
 : The difference between the p1 and the p2 is very small (lower than
1.0e-4), if the intersection point was calculated by the getIntersectionPts. : The difference between the p1 and the p2 is very small (lower than
1.0e-4), if the intersection point was calculated by the getIntersectionPts.
|
| Method |
Description |
constructor
|
public CrossCurvePT(double t1, double t2, Point2D p1, Point2D p2)
Sets the parameters to the corresponding field.
|
getParameterT1
|
public double getParameterT1()
Returns the t1 field.
|
getParameterT2
|
public double getParameterT2()
Returns the t1 field.
|
getP1
|
public Point2D getP1()
Returns the p1 field.
|
getP2
|
public Point2D getP2()
Returns the p2 field.
|
getCurvePT
|
public CurvePT getCurvePT(int index)
Parameters:
index - If the index equals 0, then it indicates the first curve, otherwise
indicates the second curve.
Returns:
If index equals 0, then returns the CurvePT object on the first curve, otherwise
returns the CurvePT object on the second curve. The both CurvePT object
is created from this object.
|
exchangeData
|
public CrossCurvePT exchangeData()
Returns the CrossCurvePT object whose curve parameters t1, t2 and p1,p2 are exchanged respectively.
|
toString
|
public String toString()
Returns the string representing this object.
|
2. Class CurvePT
return=>page top
public class CurvePT
This class represents a point on a curve by the curve parameter.
| Field |
Description |
t
|
public double t
The curve parameter represents the point.
|
p
|
Point2D p
The position (x,y) of the point.
|
| curve |
Curve2D curve
The Curve2D object on which the p is lying. |
| Method |
Description |
Constructor
|
public CurvePT(double t, Point2D p)
Sets the parameters to the corresponding field.
|
getParameter
|
public double getParameter ()
Returns the t field.
|
getP
|
public Point2D getP()
Returns the p field.
|
| selectCurvePT |
public static CurvePT selectCurvePT(Point2D p, CurvePT[] curvePTs)
Parameters:
p - The point.
curvePTs - The direction of the line to be created.
Returns:
Selects and returns the one nearest to the p from the curvePTs.
|
toString
|
public String toString()
Returns the string representing this object.
|
3. Class Curve2DUtil
return=>page top
public class Curve2DUtil
| Field |
Description |
pai
|
final static double pai=Math.PI
The circle ratio.
|
largeNumber
|
final static double largeNumber=1e+5
The large number.
|
eps10
|
final static double eps0=1e-10
The small number used for judging the convergence of Newton-Raphson method
in curve parameter.
|
eps4
|
final static double eps=1e-4
The small number.
|
eps3
|
final static double eps=1e-3
The small number.
|
The List of public methods
|
public method
|
Description |
| getIntersectionPts |
Calculates intersection points between two curves. |
| getProjectionLines |
Calculates a projected point on the curve from a given point with a
given projection vector. |
| getNormalLines |
Calculates normal lines to a curve from a given point. |
| getShortestNormalLine |
Calculates a shortest normal line to a curve from a given point.
This calculation is equal to the calculation of the closest point on the
curve from the point. |
| getShortestLine |
Calculates a shortest line to a curve from a point. |
| getNormalLinesBetweenShapes |
Calculates common normal lines between two curves.
It's also to calculate local minimum distances between two curves. |
| getShortestLineBetweenShapes |
Calculates a shortest line between two curves.
It's also to calculate minimum distances between two curves. |
| reverseCurve2D |
Returns the reversed curve. |
| trimmCurve2D |
Calculates the trimmed curve . |
| getSimpleCurve2D |
If the given curve can be converted to a simpler form - Line2DE,Polyline2DE or CubicCurve2DE, then this method converts the given curve to simpler form and returns it. |
| arrangeCurveSegment |
If successive multiple curve segments (Segment2Ds) can be united, then this method unites them to a single piece. |
| extendCurve2D |
Extends the curve by specifying the amount of extension. |
| extendCurve2DByPT |
Extends the curve at the terminal point close to the specified point(PT), so as to the line connecting the PT and the extended curve's endpoint becomes orthogonal to the extended curve. |
| createCircularArcs |
Returns the array of two Arc2D objects. The first Arc2D's endpoints are P1,P2 and the second Arc2D's endpoints are P2,P3. |
| distanceBetweenBoxes |
Calculate the distance between two Rectangle 2D objects.
|
| getMaxBox |
Returns a Rectangle2D object covering all the Rectangle2D objects given by the array.
|
| NormalsInfo |
This class is a subclass of the Curve2DUtil. It defines output data format of
the Curve2DUtil.getNormalLinesBetweenShapes method.
|
3.1 Intersection points between two curves
return=>Curve2DUtil
 =>
The formulas of the Newton-Raphson method for intersection. =>
The formulas of the Newton-Raphson method for intersection.
getIntersectionPts
(public)
|
public static CrossCurvePT[] getIntersectionPts(Curve2D curve1, Curve2D curve2)
Parameters:
curve1 - The Curve2D object of the first (parametric) curve.
curve2 - The Curve2D object of the second (parametric) curve.
Returns:
The array of the CrossCurvePT objects which represents the intersection points of the curve1 and curve2. If there is no intersection, then returns the array of 0-length.
Processing:
This method is the main method of calculating the intersection points of two curves.
First calls the boxCheck method to check the possibility of the intersection between the curve1 and curve2. If the returned value is false, then this method returns the array of
0-length, otherwise performs the following.
Second, decomposes the curve1 and curve2 into curve segments and calls the getIntersectionPtsOfSegments method to calculate the intersection between the curve segments.
Finally calls the eliminateDuplicationAndSort method to sort the intersection points according to the curve1 parameter
and remove duplicated intersection points.
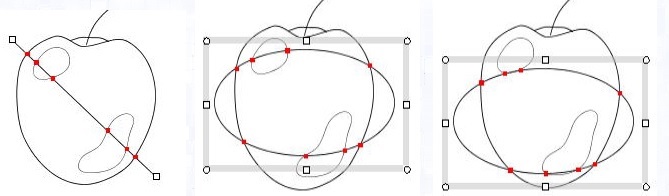
|
eliminateDuplicationAndSort
(private)
|
protected static CrossCurvePT[] eliminateDuplicationAndSort(CrossCurvePT[] PTs, double tolerance)
Parameters:
PTs - The array of the CrossCurvePT objects which represent the intersection points of the curve1 and curve2.
tolerance - The tolerance in the curve parameter space for the duplication check. Currently, 1.0e-8.
Returns:
The array of the CrossCurvePT objects in which the duplications were removed.
If there is no intersection, then returns the array of 0-length.
Processing:
Calls the indexedSimpleSort method of the Util to sort the CrossCurvePT objects and removes the duplicated intersection points with the tolerance.
|
getIntersectionPtsOfSegments
(private)
|
private static CrossCurvePT[] getIntersectionPtsOfSegments(Segment2D segment1, Segment2D segment2)
Parameters:
segment1 - The Segment2D object of the first curve segment.
segment2 - The Segment2D object of the second curve segment.
Returns:
The array of the CrossCurvePT objects which represents the intersection points of the curve1 and curve2.
If there is no intersection then returns the array of 0-length.
Processing:
Calculates the intersection points between two curve segments.
Calls the following method according to the combination of the two segment types.
⋅ The combination is LINE - LINE.
Calls the intersectionPtOfLines method which calculates the intersection by analytic method.
⋅ The combination is LINE - ARC.
Calls the intersectionPtsOfLineAndArc method which calculates the intersections by analytic method.
⋅ The combination is ARC - CUBIC, or CUBIC - CUBIC.
Calls the IntersectionPTOfArbitaries method which calculates the intersections by Newton-Raphson method.
|
intersectionPtOfLines
(private)
|
private static CrossCurvePT intersectionPtOfLines(Segment2D segment1, Segment2D segment2)
Parameters:
segment1 - The Segment2D object of the first curve segment whose type is LINE.
segment2 - The Segment2D object of the second curve segment whose type is LINE.
Returns:
The array of the CrossCurvePT objects.
If there is no intersection, then returns the array of 0-length.
Calculation of intersection points between two circular arc segments.
Processing:
The CrossCurvePT object. If there is no intersection, then returns null.
|
intersectionPtsOfLineAndArc
(private) |
private static CrossCurvePT[] intersectionPtsOfLineAndArc(Segment2D segment1, Segment2D segment2)
Parameters:
segment1 - The Segment2D object of the first curve segment whose type is LINE.
segment2 - The Segment2D object of the second curve segment whose type is ARC.
Returns:
The array of the CrossCurvePT objects.
If there is no intersection, then returns the array of 0-length.
Calculation of intersection points between two circular arc segments.
Processing:
Calculates the intersection points between a line segment and arc segment.
Let a center of an arc be Q=(Qx, Qy), its major axis be a and its minor axis be b, then the arc represented as follow:
(xーQx)2/a2 + (yーQy)2/b2 =1
(1)
The above eqation is also represented in the circular coordinates system as follow:
x=a*cosθ+Qx,y=-(b*sinθ+Qy)
(2)
Here, the minus sign of the y coordinate depends on the consideration
that the y axis is downward in the graphic coordinate system.
Let a start and an end point of a line segment be p1=(p1x, p1y) and p2=(p2x, p2y), and let the p1->p2 vectot be T=(Tx, Ty),
the equation of the line segment can be represented using the parameter t as follows.
x=Tx*t+p1x,y=Ty*t+p1y
(3)
Substitute equation (3) into equation (1) and denote P = (p1x - Qx, p1y - Qy),
then the following equation is obtained.
(Tx*t+Px)/2/a2 + (Ty*t+Py)/2/a2 = 1
(4)
Calculate the parameter t from this equation. then equation (4) can be written as follow.
c0*t2 + c1*t + c2 = 0(5)
here,
c0 = Tx2/a2 + Ty2/b2,
c1 = 2(Tx*Px/a2 + Ty*Py/b2),
c2 = Px2/a2 + Py2/b2 - 1
Solve equation (5) and get t. This parameter t is set to the CrossCurvePT object
as the line segment parameter t1.
Calculate the arc parameter t2 from equation (2).
Let the two intersection points be PT1=(PT1x, PT1y) and PT2=(PT2x, PT2y),
then the equation to get PT1 is as follow.
cosθ = (PT1x-Qx)/a, sinθ = - (PT1y-Qy)/b
Calculate θ from the above equation. Let the arc segment parameter be t2, then θ is represented as θ=start*t2+ extent.
Here the start and the extent represent the starting angle and the angular extent defined in ARC2D.
The parameter t2 can be obtained from the above equations. The calculation of the intersection point PT2 is the same as that of PT1.
|
intersectionPtsOfCircles
(static) |
private static CrossCurvePT[] intersectionPtsOfCircles(Segment2D segment1, Segment2D segment2)
Parameters:
segment1 - The Segment2D object of the first curve segment whose type is ARC.
segment2 - The Segment2D object of the second curve segment whose type is ARC.
Returns:
The array of the CrossCurvePT objects.
If there is no intersection, then returns the array of 0-length.
Calculation of intersection points between two circular arc segments.
|
intersectionPtsOfLineAndQuad
(static) |
protected static CrossCurvePT[] intersectionPtsOfLineAndQuad(Segment2D segment1, Segment2D segment2)
Parameters:
segment1 - The Segment2D object of the first curve segment whose type is LINE.
segment2 - The Segment2D object of the second curve segment whose type is QUAD.
Returns:
The array of the CrossCurvePT objects.
If there is no intersection, then returns the array of 0-length.
Calculation of intersection points between two circular arc segments.
Processing:
Calculation of intersection points between two line segment and quadratic curve segment.
|
intersectionPtsOfLineAndCubic
(static) |
protected static CrossCurvePT[] intersectionPtsOfLineAndCubic(Segment2D segment1, Segment2D segment2)
Parameters:
segment1 - The Segment2D object of the first curve segment whose type is LINE.
segment2 - The Segment2D object of the second curve segment whose type is CUBIC.
Returns:
The array of the CrossCurvePT objects.
If there is no intersection, then returns the array of 0-length.
Calculation of intersection points between two circular arc segments.
Processing:
Calculation of intersection points between two line segment and cubic curve segment.
|
intersectionPtsOfArbitraries
(private)
|
private static CrossCurvePT[] intersectionPtsOfArbitraries(Segment2D segment1, Segment2D segment2)
Parameters:
segment1 - The Segment2D object of the first curve segment whose type is arbitary.
segment2 - The Segment2D object of the second curve segment whose type is arbitary.
Returns:
The array of the CrossCurvePT objects. If there is no intersection, then returns the array of 0-length.
Processing:
First, calls the multisectionForInterSection method to execute the subdivision check for the segment1 and the segment2.
Calls the NewtonRaphsonForInterSection method for the returned intervals from the multisectionForInterSection method to calculate the intersection points accurately (1.0e-12 in parameter space).
|
multisectionFor
InterSection
(private)
|
private static void multisectionForInterSection(int depth, int numSubDiv, double delta,
Segment2D segment1, double t1s, double t1e, Segment2D segment2, double t2s, double t2e, Vector vector)
Parameters:
depth - The depth of the recursive call of this method.
numSubDiv - The number of the subdivision in x-direction and y-direction.
delta - The width and height of the subdivided segment1 and segment2 to terminate the subdivision check.
segment1 - The Segment2D object of the first curve segment.
t1s,t1e - The start and end parameters of the first curve segment to be subdivided.
segment2 - The Segment2D object of the second curve segment.
t2s,t2e - The start and end parameters of the second curve segment to be subdivided.
vector - Stores the parameter intervals of (t1s,t1e) and (t2s,t2e) to this vector, if the segment1 and the segment2 are small enough.
Processing:
First, checks the overlap between the bounding box of the segment1 and that of the segment2. If the two bounding boxes don't overlap, then returns, otherwise performs
the following step.
If the widths and heights of segment1 and the segment2 are small enough (smaller than the delta), then adds the parameter intervals of (t1s,t1e) and (t2s,t2e) to the vector and returns.
Otherwise subdivides the segment1 and calls this method recursively.
|
boxCheck
(private)
|
private static boolean boxCheck(Rectangle2D box1, Rectangle2D box2)
Parameters:
box1 - The Rectangle2D object.
box2 - The Rectangle2D object.
Returns:
True if the box1 intersects with the box2.
|
NewtonRaphsonFor
InterSection
(private)
|
private static CrossCurvePT NewtonRaphsonForInterSection(Segment2D segment1,
double t1s, Segment2D segment2, double t2s)
Parameters:
segment1 - The Segment2D object of the first curve segment.
t1s - The initial value of the segment1 for Newton-Raphson.
segment2 - The Segment2D object of the second curve segment.
t2s - The initial value of the segment2 for Newton-Raphson.
Returns:
The CrossCurvePT object. If there is no intersection, returns null.
Processing:
Convergence check
⋅ If |t1n+1-t1n|<eps and |t2n+1-t2n|<eps, then the iteration has converged.
Here the eps=1.0e-10, and the t1n, t2n are the approximated solution in parameter space of n-th
iteration.
⋅ If |p1n+1-p1n|<eps and |p2n+1-p2n|<eps1, then the iteration has converged.
Here the eps1=1.0e-4, and the p1n, p2n are the approximated intersection points in R2 of n-th iteration. The | | means distance in R2.
Error check
⋅ If the number of the iterations exceeds 10, then this method returns with error.
⋅ If the tangent vectors of the segment1 and the segment2 are parallel
at the t1n, t2n, then this method returns with error.
⋅ If one of the t1n, t2n is out of the segment range (t1n≤0, t1n≥1, t2n≤0 or t2n≥1), then this method returns with error.
|
 : The formulas of the Newton-Raphson method for intersection.
return=>Intersection points between two curves : The formulas of the Newton-Raphson method for intersection.
return=>Intersection points between two curves
Let's denote two curves as C1, C2 and their parameters
as t1, t2, then the two curves are represented as follow (A bold character represents a vector).
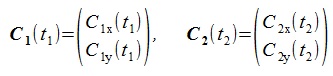
The intersection points are given by the solutions of the following equation.
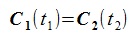
Let's defines the function f(t1, t2) as:
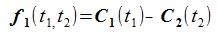
Solves the equation of f(t1, t2)=0, then we can get the intersection points.
To solve the above equation, we use the Newton-Raphson method. The iterative formula of the Newton-Raphson is described as follow:
Let dt1, dt 2 be the infinitesimals of the parameters t1, t 2 ,
then we get the following equation by using the relation of the total derivative and the partial derivatives.
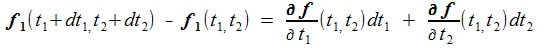 (1)
(1)
To get the iterative formula of the Newton-Raphson method, we assume
f(t1+ dt1 , t 2 + dt 2)=0in (1).
The terms of the partial derivatives in (1) are written as:
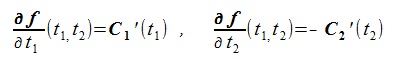
So we get the final equation as follow.
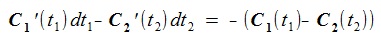
We rewrite the above equation as a matrix form:
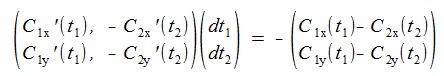 (2)
(2)
Solves the equation (2) and gets the dt1, dt2,
then replace the t1, t2
as t1+dt1-> t1, t2+dt2-> t2
and continues the iteration.
3.2 projection points on the curve from a point with a projection vector
return=>Curve2DUtil
| Method |
Description |
getProjectionLines
(public)
|
public static CurvePT[] getProjectionLines(Point2D point, Vector2D dir, Curve2D curve)
Parameters:
point - The point to be projected on the curve with the direction of dir.
dir - The Vector2D object representing the projection vector.
curve - The Curve2D object of the (parametric) curve.
Returns:
The array of the CurvePT objects which represents the endpoints of the lines normal
to the given curve. If there is no such a line, then returns the array
of 0-length.
Processing:
This method is the main method of calculating the projected points on the curve.
In other words, this method calculates the intersection points between
the infinite line passing through the given point with the same direction as the dir and the given curve.
Calls the getProjectionLineOnSegments method to calculate the projected points on the curve segments.
After that, calls the eliminateDuplicationAndSort
method to sort the projected points according to the curve parameter and remove duplicated projected points.
The figures below show the projected points on the curves
from the mouse position with the projection direction of 0°, 45°, 90° and 135°.

|
eliminateDuplication
AndSort
(private)
|
private static CurvePT[] eliminateDuplicationAndSort(CurvePT[] PTs, double
tolerance)
Parameters:
PTs - The array of the CurvePT objects which represents the endpoints of the lines normal
to the given curve.
tolerance - The tolerance in the curve parameter space for the duplication
check. Currently, 1.0e-8.
Returns:
The array of the CurvePT objects in which the duplications were removed. If there is no normal
line, then returns the array of 0-length.
Processing:
Calls the indexedSimpleSort method of the Util to sort the CurvePT objects and removes the duplicated normal points with the given tolerance.
|
getProjectionLineOn
Segment
(private)
|
private static CurvePT[] getProjectionLinesOnSegment(Point2D point, Vector2D
dir, Segment2D segment)
Parameters:
point - The point to be projected on the segment with the direction of dir.
dir - The Vector2D object representing the projection vector.
segment - The curve segment.
Returns:
The array of the CurvePT objects which represent the projected point on the
segment. If there is no such a point, then returns the array of 0-length.
Processing:
Calls the following method according to the segment type.
⋅ The type is LINE.
Calls the ProjectionToLine method which calculates the projected point by analytic method.
⋅ The type is ARC without an affine transform.
Calls the ProjectionToCircularArc method which calculates the projected points by analytic method.
⋅ The type is CUBIC or ARC with an affine transform.
Calls the ProjectionToArbitary method which calculates the projected points by bisection method
and Newton-Raphson method.
|
ProjectionToLine
(private)
|
private static CurvePT ProjectionToLine(Point2D point, Vector2D dir, Segment2D
segment)
Parameters:
point - The point to be projected on the segment with the direction of dir.
dir - The Vector2D object representing the projection vector.
segment - The line segment (Segment2D object).
Returns:
The CurvePT object representing the projected point on the segment. If there is no projected point, then returns null.
|
ProjectionToCircular
Arc
(private)
|
private static CurvePT[] ProjectionToCircularArc(Point2D point, Vector2D
dir, Segment2D segment)
Parameters:
point - The point to be projected on the segment with the direction of dir.
dir - The Vector2D object representing the projection vector.
segment - The circular arc segment (Segment2D object).
Returns:
The array of the CurvePT objects representing the projected points on the segment. If there is no such a point, then returns the array of 0-length.
|
ProjectionToArbitrary
(private)
|
private static CurvePT[] ProjectionToArbitrary(Point2D point, Vector2D
dir, Segment2D segment)
Parameters:
point - The point to be projected on the segment with the direction of dir.
dir - The Vector2D object representing the projection vector.
segment - The Segment2D object of the curve segment.
Returns:
The array of the CurvePT objects representing the projected points on the segment. If there is no such a point, then returns the array of 0-length.
Processing:
First, subdivides the segment parameter interval (0≤t≤1) into
small intervals and calls the the bisectionForProjectionLine method
for each small interval.
Calls the NewtonRaphsonForProjectionLine method for the returned intervals from the bisectionForProjectionLine method to calculate the projected point accurately.
|
bisectionFor
ProjectionLines
(private)
|
private static void bisectionForProjectionLine(Point2D point, Vector2D
dir, Segment2D segment, double ts, double te, Vector vector)
Parameters:
point - The point to be projected on the segment with the direction of dir.
dir - The Vector2D object representing the projection vector.
segment - The Segment2D object of the curve segment.
ts,te - The start and end parameters of the curve segment to be subdivided.
vector - Stores the parameter interval of [ts,te] to this vector, if the segment is small enough.
Processing:
If there is a possibility that the projected point exists in the [ts, te] interval
and the interval is small, then saves the interval to the vector and returns.
If the interval is not small enough, then subdivides this
interval and calls this method recursively. If there is no possibility
that the projected point exists in the [ts, te], then returns.
|
NewtonRaphsonFor
ProjectionLines
(private)
|
private static CurvePT NewtonRaphsonForProjectionLine(Point2D point, Vector2D
dir, Segment2D segment, double ts, double te)
Parameters:
point - The point to be projected on the curve with the direction of dir.
dir - The Vector2D object representing the projection vector.
segment - The Segment2D object of the curve segment.
ts,te - The start and end parameters of the curve segment to be subdivided.
Returns:
The CurvePT object. If there is no projected point, returns null.
Processing:
Convergence check
⋅ If the |tn+1-tn|<eps, then the iteration has converged.
Here the eps=1.0e-12.
Error check
⋅ If the number of the iterations exceeds 10, then returns with error.
⋅ If the f'(tn) of equals 0, then returns with error.
⋅ If the tn is out of the [ts,te], then returns with error.
|
3.3 Normal lines to a curve from a point
return=>Curve2DUtil
 =>
The formulas of the Newton-Raphson method for normal lines =>
The formulas of the Newton-Raphson method for normal lines
| Method |
Description |
getNormalLines
(public)
|
public static CurvePT[] getNormalLines(Point2D point, Curve2D curve)
Parameters:
point - The given point.
curve - The Curve2D object of the (parametric) curve.
Returns:
The array of the CurvePT objects representing the points on the curve. The lines connecting the given point and the points to be returned must be normal to the curve. If there is no such a point, then returns the array of 0-length.
Processing:
This method is the main method of calculating the normal lines to the given
curve that pass the given point.
Calls the getNormalLinesOnSegments method to calculate the normal lines to the curve segments and returns
the endpoints of the lines.
After that, calls the eliminateDuplicationAndSort method to sort the endpoints of the lines according to the curve parameter
and remove duplicated normal points.
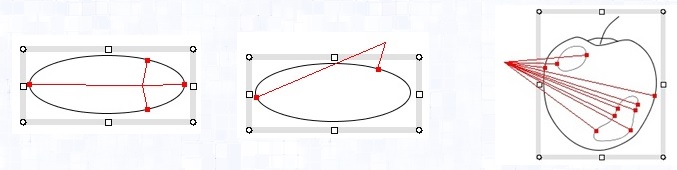
|
getNormalLinesOn
Segment
(private)
|
private static CurvePT[] getNormalLinesOnSegment(Point2D point, Segment2D segment)
Parameters:
point - The given point.
segment - The curve segment.
Returns:
The array of the CurvePT objects which represents the endpoints of the normal lines to the given
segment. If there is no such a line, then returns the array of 0-length.
Processing:
Calculates the normal lines to the given segment. Calls the following method
according to the segment type.
⋅ The type is LINE.
Calls the NormalToLine method
which calculates the line normal to a line segment by analytic method.
⋅ The type is ARC and a circular arc, not an elliptic arc.
Calls the NormalToCircularArc method
which calculates the line normal to a circular arc segment by analytic method.
⋅ The type is CUBIC or ARC(an elliptic arc).
Calls the NormalToArbitary method
which calculates the line normal to an arc or cubic segment by Newton-Raphson method.
|
NormalToLine
(private)
|
private static CurvePT NormalToLine(Point2D point, Segment2D segment)
Parameters:
point - The given point.
segment - The line segment.
Returns:
The CurvePT object which represents the endpoint of the normal line
to the given line segment. If there is no normal line, then returns null.
|
NormalToCircularArc
(private)
|
private static CurvePT[] NormalToCircularArc(Point2D point, Segment2D segment)
Parameters:
point - The given point.
segment - The circular arc segment.
Returns:
The CurvePT objects which represents the ending points of the normal lines
to the given arc segment. If there is no such a line, then returns the
array of 0-length.
|
NormalToArbitrary
(private)
|
private static CurvePT[] NormalToArbitrary(Point2D point, Segment2D segment)
Parameters:
point - The given point.
segment - The Segment2D object of the curve segment.
Returns:
The array of the CurvePT objects which represent the endpoints of the normal lines
to the given curve segment. If there is no such a line, then returns the
array of 0-length.
Processing:
First, subdivides the segment parameter interval (0≤t≤1) into
small intervals, and calls the bisectionForNormalLines method for each small interval.
If a normal line is found in the interval, then calls the NewtonRaphsonForNormalLines method to calculate the en point of the normal line accurately.
|
bisectionForNormalLines
(private)
|
private static void bisectionForNormalLines(Point2D point, Segment2D segment, double ts, double te, Vector vector)
Parameters:
point - The given point.
segment - The Segment2D object of the curve segment.
ts,te - The start and end parameters of the curve segment to be subdivided.
vector - Stores the parameter interval of [ts,te] to this vector, if the segment is small enough.
Processing:
First, calculates the values of the formula (3) on this page at ts and te. If the two values have different signs, then the normal line may be exists
in the [ts, te] interval, otherwise this method returns.
If the [ts, te] interval is small enough, then adds the interval to the vector. Otherwise subdivides the curve segment and calls this method recursively.
|
NewtonRaphsonForNormalLines
(private)
|
private static CurvePT NewtonRaphsonForNormalLines(Point2D point, Segment2D segment, double ts, double te)
Parameters:
point - The given point.
segment - The Segment2D object of the curve segment.
ts,te - The start and end parameters of the curve segment in which the Newton-Raphson
will be executed.
Returns:
The CurvePT object. If there is no point, returns null.
Processing:
Convergence check
⋅ If |tn+1-tn|<eps, then the iteration has converged.
Here the eps=1.0e-10.
Error check
⋅ If the number of the iterations exceeds 10, then this method returns with error.
⋅ If the f'(tn) of (5) equals 0, then this method returns with error.
⋅ If the tn is out of the range (tn≤ts or tn≥te), then this method returns with error.
|
 :
The formulas of the Newton-Raphson method for normal lines
return=>Normal lines to a curve from a point :
The formulas of the Newton-Raphson method for normal lines
return=>Normal lines to a curve from a point
Let's denote the curve as C(t) and the given point as P , and define the function f(t) as:
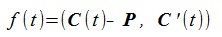 (x,y): scalar product,
P: the given point, C'(t): derivative
(3)
(x,y): scalar product,
P: the given point, C'(t): derivative
(3)
Solves the equation of f(t)=0 , then we can get
the endpoints of the lines normal to the curve that pass the given P .
Let dt be the infinitesimal of the parameters t, then we get the following equation.
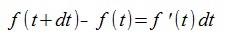
To get the iterative formula of the Newton-Raphson method, we assume
f(t+ dt)=0 in the above equation.
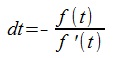 (4)
(4)
Here, 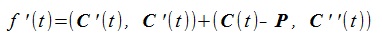 (5)
(5)
Solves the equation (4) and gets the dt , then replace the t as t+dt->t and continues the iteration.
3.4 Shortest normal line to a curve from a point
return=>Curve2DUtil
| Method |
Description |
getShortestNormalLine
(public)
|
public static CurvePT getShortestNormalLine(Point2D point, Curve2D curve)
Parameters:
point - The given point.
curve - The Curve2D object of the (parametric) curve.
Returns:
The CurvePT objects representing the nearest point on the curve. The line connecting the given point and the nearest point must be normal to the curve. If there is no such a line, then returns the array of 0-length.
Processing:
Calls the getNormalLines method. If multiple points are found, returns the nearest one.
|
3.5 Shortest line to a curve from a point
return=>Curve2DUtil
| Method |
Description |
getShortestLine
(public)
|
public static CurvePT getShortestLine(Point2D point, Curve2D curve)
Parameters:
point - The given point.
curve - The Curve2D object of the (parametric) curve.
Returns:
The CurvePT object representing the nearest point on the curve from the given point.
The line connecting the given point and the nearest point doesn't need to be normal to the curve.
Processing:
First, calls the getShortestNormalLine method and gets the nearest normal point on the curve.
Second, selects the nearest segment junction point of the curve from the given point.
Finally, selects the nearest one from the nearest two points and returns it.
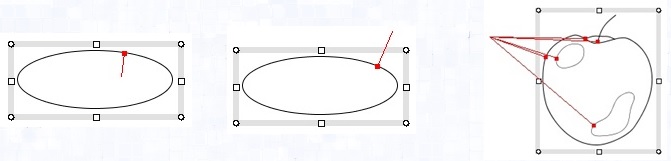
 : Calculation notes : Calculation notes
|
| (a)The segment junction point is nearest |
(b)The normal point is nearest |
|
3.6 Common normal lines between two shapes
return=>Curve2DUtil
 =>
Processing Method =>
Processing Method
Method
|
Description
|
getNormalLinesBetweenShapes
(static)
|
public static Vector getNormalLinesBetweenShapes(Curve2D curve1, Curve2D curve2,
String shapeId1, String shapeId2)
Parameters:
curve1 - Curve2D object.
curve2 - Curve2D object.
shapeId1 - The shapeId of the ShapeContainer which outline curve is the curve1.
shapeId2 - The shapeId of the ShapeContainer which outline curve is the curve2.
Returns:
Returns a vector storing the NormalsInfo objects in which common normal lines and intersection points are stored.
Processing:
Decomposes the curve1 and curve2 to curve segments
and calls the segmentsNormalLinesBetweenLines,
segmentsNormalLinesBetweenCircles
or segmentsNormalLinesBetweenArbitraries methods.
Before the end of this method, calls the eliminateNormalLinesDuplication method bellow
to removes the dupulication between the output data of NormalsInfo objects.

 : The method can also get intersection points between the curve1 and the curve2 : The method can also get intersection points between the curve1 and the curve2
|
eliminateNormalLinesDuplication
(static)
|
protected static Vector eliminateNormalLinesDuplication(Vector normalsVector)
Removes the duplication between NormalsInfo objects stored in
the normalsVector(given as the parameter)
|
segmentsNormalLinesBetweenLines
(static)
|
protected static Vector segmentsNormalLinesBetweenLines(Segment2D segment1, Segment2D segment2)
Parameters:
segment1 - Segment2D object
segment2 - Segment2D object
Returns:
Vector - Stores a NormalsInfo object
which stores the common normal line or the intersection point between the segment1 and the segment2.
Processing:
Calculating a common normal line between two line segments.
∙ Calculating a common normal line:
A common normal line exists, if two line segments are parallel.
If they are not parallel, then returns without doing anything.
If they are parallel, gets the fee of normal line from the both endpoints of one line segment to another
by the Curve2DUtil.ProjectionToLine method
and calculates the curve interval on which common normal line exists.
Sets type=SegmentIntervalSolution
to the output data of a NormalsInfo object.
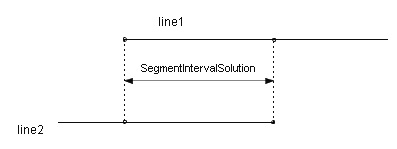
A common normal line exists on the intervals indicated by the arrow.
∙ Calculating a intersection point:
Gets a intersection point by the Curve2DUtil.intersectionPtOfLinesでmethod
and stores a NormalsInfo to vector object.
|
segmentsNormalLinesBetweenCircles
(static) |
protected static Vector segmentsNormalLinesBetweenCircles(Segment2D segment1, Segment2D segment2)
Parameters:
segment1 - Segment2D object
segment2 - Segment2D object
Returns:
Vector - Stores a NormalsInfo object
which stores the common normal line or the intersection point between the segment1 and the segment2.
Processing:
Calculating a common normal line between two circular segments.
∙ Calculating a common normal line (1):
This is the case when the centers of segment1 and segment2 are equal.
Gets the feet of normal line from the both endpoints of one circular segment to another
and calculates the curve interval on which common normal line exists.
Sets type=SegmentIntervalSolution
to the output data of a NormalsInfo object.
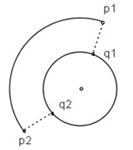
The common normal line exists from the p1-p2 interval to the q1-q2 interval.
∙ Calculating a common normal line (2):
This is the case when the centers of segment1 and segment2 aren't equal.
The common normal lines lie on the connecting line from the center of segment1 to that of segment2.
So the common normal lines can be got to extend that connecting line to the segment1 arc and senment2 arc.
If the segment1 and the segment2 are full circles, the four common normal lines can be found.
 =>
Java Drawing Test Codes Figure 3.3 =>
Java Drawing Test Codes Figure 3.3
Sets the type=SegmentSolution to output NormalsInfo objects.
∙ Calculating intersection points:
Calculates them by the Curve2DUtil.intersectionPtsOfCircles method,
and returns the NormalsInfo objects.
|
segmentsNormalLinesBetweenArbitraries
(static)
|
protected static Vector segmentsNormalLinesBetweenArbitraries(Segment2D segment1, Segment2D segment2)
Parameters:
segment1 - Segment2D object
segment2 - Segment2D object
Returns:
Vector - Stores a NormalsInfo object
which stores the common normal line or the intersection point between the segment1 and the segment2.
Processing:
Calculates the common normal lines between arbitrary segments.
Divides the segments1, 2
and executes the Step1 described in the Processing Method
to find segment intervals in which common normal lines may exist by the next roughCheck method.
When the division becomes sufficiently fine, then calculates common normal lines very accurately
by the NewtonRaphsonForNormalLinesBetweenShapes method.
|
roughCheck
(static)
|
protected static void roughCheck(int depth, double stopSize, int[] numDiv,
Segment2D segments[], double[] T, Vector normalsVector)
Parameters:
depth - The depth of the recursive call of this method.
stopSize - The division sizes of the segments to stop the recursive call of this method.
 : The division sizes are the sizes of the bounding boxex which cover the segments. : The division sizes are the sizes of the bounding boxex which cover the segments.
numDiv - The division number of the segments.
The numDiv[0] is the division number of the segments[0] and the numDiv[1] is that of the segments[1].
segments - Stores the curve segment1 and the curve segment2.
T - The curve segment parameters which represent the divided intervals of the segments.
The T[0] and T[1] represent the start and end parameters of the segments[0], and the T[2] and T[3] represent that of the segments[1].
normalsVector - Stores the interval in which the common normal lines may exist
to a NormalsInfo object and save it to this vector.
Sets the type=SegmentHitInterval to the NormalsInfo object.
Returns:
Vector - Stores the NormalsInfo objects.
Processing:
 =>
Processing Method,
2.1 Processing, 2.2 Formulas,
Figure 2.1, 2.2, Figure 2.3 =>
Processing Method,
2.1 Processing, 2.2 Formulas,
Figure 2.1, 2.2, Figure 2.3
∙ This method is called recursively.
∙ Tests whether common normal lines exist or not by the next segmentHit method.
If there is a possibility of existence of common normal lines between the segments[0] and segment[1],
then creates a NormalsInfo object
which type is SegmentHitInterval
and stores it to the normalsVector and calls this method recursively.
At this time, the parameter of the depth is set to (depth+1).
∙ Stop condition
Divides the segment interval by the bisection method
and stop the bisection if the width and height of the segment intervals become smaller than the stopSize.
Then stores the segment intervals to the normalsVector
as the NormalsInfo objects and returns.
|
segmentHit
(static)
|
protected static boolean segmentHit(Segment2D segment1, Segment2D segment2, double[] newT)
Parameters:
segment1 - Segment2D object
segment2 - Segment2D object
newT - The curve segment parameters which represent the divided intervals of the segment1 and segment2.
The T[0] and T[1] represent the start and end parameters of the segment1,
and the T[2] and T[3] represent that of the segment2.
Returns:
boolean - Returns true if there is a possibility of having that common normal lines lie
between the segment1 and segment2.
Processing:
Hit test of this method is mainly done by the next rectHit methid.
|
rectHit
(static)
|
protected static boolean rectHit(Point2D p1, Point2D p2, Vector2D e1, Vector2D e2, Rectangle2D rect)
Parameters:
p1 - An endpoint of a segment interval.
p2 - Another endpoint of a segment interval.
e1 - The unit normal vector to the segment at p1.
e2 - The unit normal vector to the segment at p2.
rect - A rectangle to be tested.
Returns:
int - Returns true if the part of the rect lies in the Region A or B (see the Figure 3.1(c) below).
Processing:
Executes the above test for the four corner points of the rect.
If at least one of the corner points is belongs to the Region A or B, return true.
And if one corner point belongs to the Region C and another belongs to the Region D, return true.
 =>
Java Drawing Test Codes, Common normal lines between two shapes, Figure 3.1(c). =>
Java Drawing Test Codes, Common normal lines between two shapes, Figure 3.1(c).
|
ptPosition
(static)
|
public static int ptPosition(Point2D p1, Point2D p2, Vector2D e1, Vector2D e2, Point2D p)
Parameters:
p1 - A endpoint of a segment interval.
p2 - Another endpoint of a segment interval.
e1 - The unit normal vector to the segment at p1.
e2 - The unit normal vector to the segment at p2.
p - The point to be tested.
Returns:
int - The number of the region which the p belongs to (Region A/B/C/D=1/2/3/4)
Processing:
 =>
2.1 Processing steps, Figure 2.1, 2.2, Figure 2.3 =>
2.1 Processing steps, Figure 2.1, 2.2, Figure 2.3
|
NewtonRaphsonForNormalLinesBetweenShapes
(static)
|
protected static NormalsInfo NewtonRaphsonForNormalLinesBetweenShapes(Segment2D segment1, Segment2D segment2,
double t1s, double t2s)
Parameters:
segment1 - Segment2D object
segment2 - Segment2D object
t1s, t1e - The start and end segment parameters of the segment1 interval where a common normal line may exist.
t2s, t2e - The start and end segment parameters of the segment2 interval where a common normal line may exist.
Returns:
Stores the segment parameter to a NormalsInfoobject and returns it.
Here, the type=SegmentSolution is set to the NormalsInfo object.
Convergence check:
⋅ The dt1 and dt2 which are differences to the previous iteration becomes under 1.0e-12,
then stops the Newton-Raphson iteration. And so on.
 =>
2.2.2 Newton Raphson method and the formulas for Step3 =>
2.2.2 Newton Raphson method and the formulas for Step3
Error checks
⋅ Error when the number of the Newton-Raphson iterations becomes over 10 times.
⋅ Error when the segment parameter t1 or t2 going outside the interval [t1s, t1e] or [t2s, t2e].
And so on.
|
 : Processing Method
return=>Common normals between two shapes : Processing Method
return=>Common normals between two shapes
1. Related Documents
 =>
Java Drawing Test Codes: Common normal lines between two shapes =>
Java Drawing Test Codes: Common normal lines between two shapes
The above document includes the test results.
2. Processing method
2.1 Processing steps(Figure 2.1, 2.2)
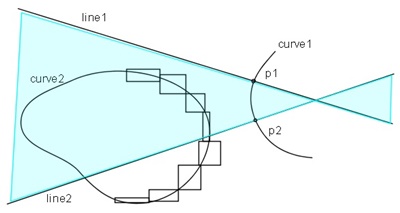
Step1. Test for possible existence of common normal lines
First, divides the curve1 to small segments as shown in Figure 2.1 so as not to have inflection points.
Next, creates the normal lines which are line1, line2 at the end points of the small segment.
At the same time, divides the curve2 to small segments and cover each small segment by a rectangle (bounding box).
Here, if the all or part of the bounding box which covers the small segment of the curve2 exists
in the sandwiched area by the line1 and line2 (light blue area in Figure 2.1),
then there is a possibility that the small segment of curve2 and the segment
of the curve1 delimited by p1 and p2 has a common normal line.
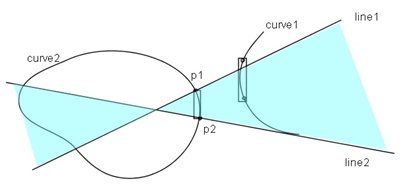
Moreover exchanges the standpoint of curve1 and the curve2 and executes the same test as shown in Figure 2.2,
the more accurate possibility for the existence of common normal lines will be given.
Step2. Bisection method to get the higher possibility for the existence of common normal lines
Bisects the couple of segments of the curve1 and curve2 which may have common normal lines
and executes the same test described in Step1.
Repeats this process by recursive call until the divided segments become enough small.
Step3. High accurate computation by Newton Raphson method
Sets the center points of the enough small segments of the curve1 and curve2
as the initial points and executes the Newton Raphson method.
 |
 |
| Figure 2.1 Test for possible existence of a common normal lines(1) |
Figure 2.2 Test for possible existence of a common normal lines(2) |
2.2 Formulas
returns=>Common normals between two shapes
2.2.1 Formulas for Step1
(Figure 2.3(a)-(e))
To test that the all or part of the bounding box exists in the sandwiched area (light blue area in Figure 2.1),
it is enough to test whether each of the vertexes of the bounding box is exist in the sandwiched area or not.
The following (a)-(d) describes the case that line1 and line2 are not parallel,
and the (e) describes the case that they are parallel.
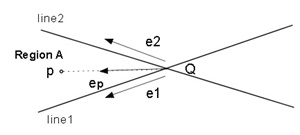
Let e1 and e2 be the unit normal vectors of the line1 and line2 directions,
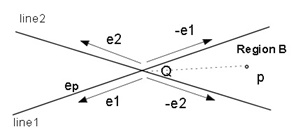
and let ep be the unit vector headed from the point Q to the point p shown as Figure 2.3(a).
Here the point Q is the intersection point between the line1 and line2.
We find the condition that the point p exists in the "Region A".
The outer product between two 2D vectors can be defined in the similar way of that of 3D vectors as follows;
e1×e2 =e1x * e2y -
e1y * e2x(1)
Here, the e1×e2 corresponds to z-value of the outer product between two 3D vectors
and the e1×e2 represents the signed area of the parallelogram spanned
by e1 and e2.
Additionally we assume e1×e2≧0 (if not, exchanges e1 and e2).
 :
In the normal coordinate, e1×e2≧0 is satisfied
if the rotation from e1 to e2 is counter clockwise,
however in the graphic coordinate, the outer product≧0 is satisfied if the rotation is clockwise,
because the y-axis is downward. :
In the normal coordinate, e1×e2≧0 is satisfied
if the rotation from e1 to e2 is counter clockwise,
however in the graphic coordinate, the outer product≧0 is satisfied if the rotation is clockwise,
because the y-axis is downward.
(a) The condition that the point p exists in the Region A (Figure 2.3(a)).
0≦e1×ep ≦e1×e2 and 0≦ep×e2 ≦e1×e2(2)
(b) The condition that the point p exists in the Region B (Figure 2.3(b)).
0≦(-e1)×ep≦(-e1)×(-e2) and 0≦ep×(-e2)≦(-e1)×(-e2)
=> -(e1×e2)≦e1×ep≦0 and -(e1×e2)≦ep×e2≦0(3)
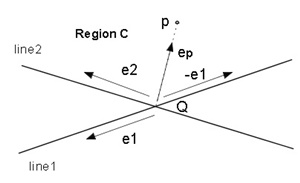
(c) The condition that the point p exists in the Region C (Figure 2.3(c)).
0≦ep×(-e1)≦e2×(-e1) and 0≦e2×ep≦e2×(-e1)
=> 0≦e1×ep≦e1×e2 and 0≦-(ep×e2)≦e1×e2
=> 0≦e1×ep≦e1×e2 and -(e1×e2)≦ep×e2≦0(4)
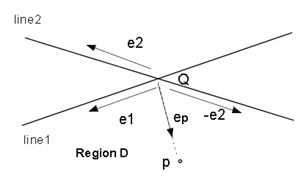
(d) The condition that the point p exists in the Region D (Figure 2.3(d)).
0≦ep×e1≦(-e2)×e1 and 0≦(-e2)×ep≦(-e2)×e1
=> 0≦-(e1×ep)≦e1×e2 and 0≦ep×e2≦e1×e2
=> -(e1×e2)≦e1×ep≦0 and 0 ≦ep×e2≦e1×e2(5)
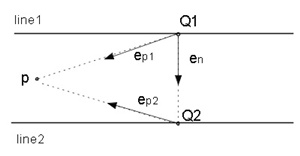
(e) The condition that the point p exists in the sandwitched area between line1 and line2 (Figure 2.3(e)).
Let define the unit vectors: ep1, ep2 and ep shown as Figure 2.3(e), then the condition is following.
0≦en×ep1≦|Q2-Q1| (6)
Here, |Q2-Q1| is the distance between line1 and line2.
 => The test results are shown in
Java Drawing Test Codes Figure 3.1, 3.2. => The test results are shown in
Java Drawing Test Codes Figure 3.1, 3.2.
(a) |
(b) |
(c) |
(d) |
(e) |
|
| Figure 2.3 Formulas for Step1 |
2.2.2 Newton Raphson method and the formulas for Step3
returns=>Common normals between two shapes
Let t1 and t2 be the parameters of C1 and C2 curves
and represents these curves by their x, y components as follows:
Here, bold types represent vectors.
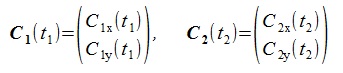 (1) (1)
To get a common normal line between two curves, we have to find the t1, t2
which achieve the local minimum of the distance between two curves. The following f1(t1, t2)
is the square of the distance between C1 and C2.
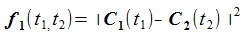 (2) (2)
The following condition is required to minimize the f1(t1, t2) (<a, b> is inner product of vector a and vector b).
 (3) (3)
Let f1(t1, t2), f2(t1, t2)
be the right side of the abve (3) (ignoring coefficient). then,
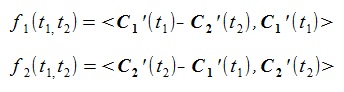 (4) (4)
Let dt1, dt2 be very small values or infinitesimals(dt1, dt2 are written as Δt1, Δt2 in a textbook),
then the following formulas are derived from the relations between total differential
and partial differential for the f1(t1),
t2, f2(t1,t2).
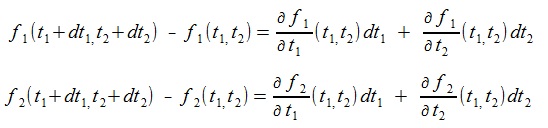 (5) (5)
Here, the right sides of (5) are represented as follows:
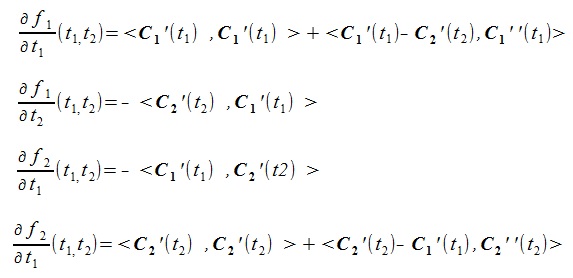 (6) (6)
The approximation formula of the NewTon-Raphson method is given by setting parts of the left sides of (5) equal 0(zero) as follows.
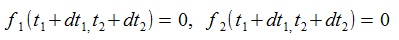 (7) (7)
(5) can be written as follows:
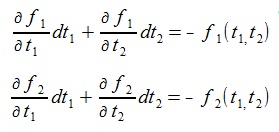 (8) (8)
The matrix representation of (8) is followings:
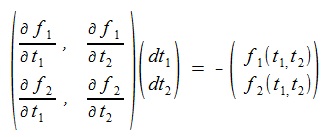 (9) (9)
Let D be the matrix of the left side of (9):
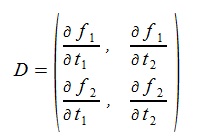 (10) (10)
The dt1, dt2 are given by solving (9) as follows (det means determinant):
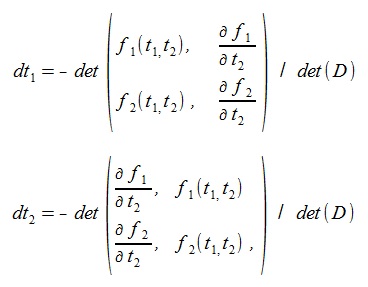 (11) (11)
3.7 Shortestline between two shapes
戻る=>Curve2DUtil
Method
|
Description
|
getShortestLineBetweenShapes
(public) |
public static Vector getShortestLineBetweenShapes(Curve2D curve1, Curve2D curve2,
String shapeId1, String shapeId2)
Parameters:
curve1 - Curve2D object.
curve2 - Curve2D object.
shapeId1 - The shapeId of the ShapeContainer which outline curve is the curve1.
shapeId2 - The shapeId of the ShapeContainer which outline curve is the curve2.
Returns:
Returns a vector storing the NormalsInfo objects in which shortest and intersection points are stored.
Processing:
∙ Calculate common normal lines between the curve1 and the curve2.
The above processing is executed by the Curve2DUtil.getNormalLinesBetweenShapes method
and this method stores its output data(NormalsInfo objects)
to the Vector object(infos).
∙ Calculate shortest lines from the curve1 segment points to the curve2.
This processing is executed by the the Curve2DUtil.getShortestLine
and this method converts the output data represented by a CurvePT object
to a NormalsInfo object and stores it in the Vector object(infos).
∙ Calculate shortest lines from the curve2 segment points to the curve1.
This processing is the same as the above.
∙ Set the reurn value.
Select a shortest line and intersection points from the infos,
stores their NormalsInfo objects
to another Vector object and return it.

 : :
∙ The Curve2DUtil.getNormalLinesBetweenShapes
method can also calculates inpersention points.
∙ Since the Curve2DUtil.getShortestLine
method calculates the distances between segment points of the curve1 and those of curve2,
the method can get the shortest line that connects the cusp points of the shapes.
|
3.8 Reverse a curve
return=>Curve2DUtil
| Method |
Description |
| reverseCurve2D |
public static Curve2D reverseCurve2D(Curve2D curve)
Parameters:
curve - Curve2D object
Returns:
Returns the reversed curve.
|
3.9 Trim a curve
return=>Curve2DUtil
| Method |
Description |
trimCurve2D
(public)
|
public static Curve2D trimCurve2D(Curve2D curve, double t1, double t2)
Parameters:
curve - The Curve2D object of the (parametric) curve.
t1,t2 - The trimming interval.
Returns:
The Curve2D object which represents the trimmed curve.
Processing:
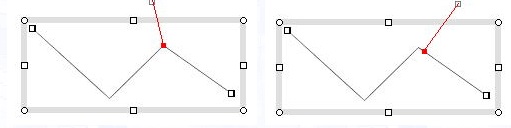
If the curve is not closed, calls this method with the parameters of t1<t2.
If the curve is closed and t1>t2, then connects the trimmed curve of the interval [t1,te]
with the trimmed curve of the interval [ts,t2], and returns the connected curve.
In the left figure below, the arrow-shaped polygon is composed of seven line segments,
so the order of ts, {ti}, te is ts=0.0<t0<t1<t2<t3<te=7.0.
The cutting sections are [t0,t1], [t1,t2], [t2,t3], [t3,t0], and the four polylines are created.
The right figuret below is the result, and it is shown by shifting the four polylines
little by little to make them easy to see.
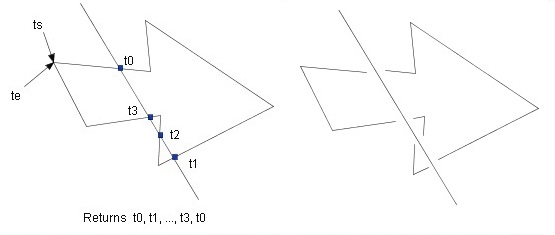
|
3.10 Translate curve to simple form, if possible
return=>Curve2DUtil
| Method |
Description |
getSimpleCurve2D
(public) |
public static Curve2D getSimpleCurve2D(Curve2D curve)
Returns:
The Curve2D object of simpler form.
Processing:
If the given curve can be converted to a simpler form - Line2DE,Polyline2DE
or CubicCurve2DE, then this method converts the given curve
to simpler form and returns it.
|
3.11 Unit curves
return=>Curve2DUtil
| Method |
Description |
arrangeCurveSegment
(public) |
public static Curve2D arrangeCurveSegment(Curve2D curve)
Parameters:
curve - Curve2D object
Returns:
Returns the Curve2D object. If any segments aren't united, then return
the clone of the curve specified by parameter.
Processing:
If successive multiple curve segments (Segment2Ds) can be united, then this method unites them to a single piece.
In reality, if an ellipse (or circle) is divided into two parts by a straight
line, the part containing start and end points of the ellipse will consists
of two arcs. This method can unites such two arcs.
|
uniteSegment2Ds
(private) |
private static Segment2D uniteSegment2Ds(Segment2D segment1, Segment2D segment2)
Parameters:
segment1 - Segment2D object.
segment2 - Segment2D object.
Returns:
If the segment1and the segment2 can be united, returns the united segment.
If the two segments can't be united, returns null.
Processing:
This method is called from arrangeCurveSegment method. The processing will be done if the
segment1 and segment2 are lines or arcs.
|
3.12 Extend a curve by the specified extension
return=>Curve2DUtil
| Method |
Description |
extendCurve2D
(public) |
public static Curve2D extendCurve2D(Curve2D curve, double extension, int
pos)
Parameters:
curve - Curve2D object
extension - The amount of extension.
pos - 0: extends the curve at the start point. 1: extends the curve at the
end point.
Returns:
Returns the extended Curve2D object.
Processing:
This method extends the given curve (curve). This method calls extendSegment2D method. So if
the curve is extended at the start point, the reverseCurve2D method must be called to reverse the direction of the curve before calling extendSegment2D.
|
extendSegment2D
(private) |
private static Segment2D extendSegment2D(Segment2D segment, double extension)
Parameters:
segment - Segment2D object
extension - The amount of extension.
Returns:
segment is a Line2D or Arc2D segment:extends the segment at the end point and return the segment.
segment is a CubicCurve2D segment:creates a new segment that connect to
the segment at the end point and return the new segment. The new segment is a CubicCurve2D segment which direction at the start
point equals the direction of the segment at the end point.
Processing:
This method is called from extendCurve2D. This method extends the segment at the end point.
|
3.13 Extend a curve to a specified point
return=>Curve2DUtil
| Method |
Description |
extendCurve2DByPT
(public) |
public static Curve2D extendCurve2DByPT(Curve2D curve, Point2D PT)
Parameters:
curve - Curve2D object
PT - Extends the curve at the terminal point close to the PT,
so as to the line connecting the clicked point(PT)
and the extended curve's endpoint become orthogonal to the extended curve.
Returns:
Returns the extended Curve2D object.
Processing:
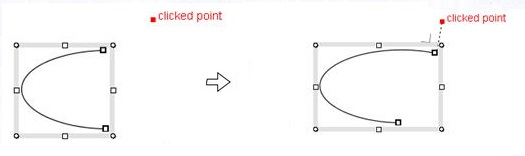
|
extendSegment2D
ByPT
(private) |
private static Segment2D extendSegment2DByPT(Segment2D segment, Point2D
PT)
Parameters:
segment - Segment2D object
PT - same as the PT of extendCurve2DByPT
Returns:
segment is a Line2D or Arc2D segment:extends the segment at the end point and return the segment.
segment is a CubicCurve2D segment:creates a new segment that connect to
the segment at the end point and return the new segment. The new segment is a CubicCurve2D segment which direction at the start
point equals the direction of the segment at the end point.
|
3.14 creating circles by specified three points
return=>Curve2DUtil
| Method |
Description |
createCircularArcs
(private)
|
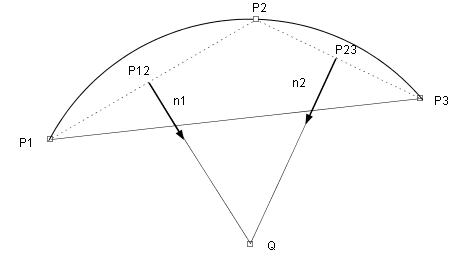
public static Arc2D[] createCircularArcs(Point2D p1, Vector2D tangent1,
Point2D p2, Vector2D tangent2)
Parameters:
p1,p2,p3 - The three points of the arc to be created
Returns:
The array of two Arc2D objects. The first Arc2D's endpoints are P1,P2 and
the second Arc2D's endpoints are P2,P3 in the figure below.
If the P1,P2 and P3 lie on a straight line, returns the array of 0-length.
Processing:
P12: The middle point of the line of P1, P2.
P23: The middle point of the line of P2, P3.
n1: The normal line to the line of P1, P2 and passing P12.
n2: The normal line to the line of P2, P3 and passing P23.
Q: the center of the arc passing P1,P2 and P3.
This method calculates the above points and lines, and finally creates
the two Arc2D objects.
|
getCrossPoint
(static)
|
private static Point2D getCrossPoint(Vector2D p1, Vector2D n1, Vector2D
p2, Vector2D n2)
Parameters:
p1,p2,p3 - The three points of the arc to be created
Returns:
The center point Q (the figure above) of the arc.
Processing:
Calculates the intersection point of the line n1 and n2 and returns the
point.
|
3.15 distanceBetweenBoxes
戻る=>Curve2DUtil
Method
|
Description
|
distanceBetweenBoxes
(private)
|
public static double distanceBetweenBoxes(Rectangle2D box1, Rectangle2D box2)
Returns the distance between box1 and box2. The distance is 0 when box1 and box2 overlap.
|
3.16 getMaxBox
戻る=>Curve2DUtil
メソッド
|
説明
|
getMaxBox
(private)
|
public static Rectangle2D getMaxBox(Rectangle2D[] boxes)
Returns the smallest Rectangle2D covering all the boxes given by the array.
|
3.17 NormalsInfo subclass
return=>Curve2DUtil
| Method |
Description |
type
|
public int type = 0;
Set a value from the following constants: Solution―SegmentHitInterval.
|
Solution
|
public final static int Solution = 0;
Sets this constant value to the type field when the getNormalLinesBetweenShapes method
stores its solution between two curves that are Curve2Ds to this object.
|
IntervalSolution
|
public final static int IntervalSolution = 1;
Sets this constant value to the type field
when the getNormalLinesBetweenShapes method
stores its solution to this object.
The solution can be found as an interval when the target shapes: curve1 and curve2 are
the combination of a line and a line or the combination of a circular arc and a circular arc.
|
SegmentPtSolution
|
public final static int SegmentPtSolution = 2;
This constant isn't used currently.
|
SegmentSolution
|
public final static int SegmentSolution = 3;
Sets this constant value to the type field
when the methods to receive segments as parameters store their solution to this object.
Here, the segments above mentioned are Segment2D objects
and the methods to receive segments as parameters are:
segmentsNormalLinesBetweenLines,
segmentsNormalLinesBetweenCircles and
segmentsNormalLinesBetweenArbitraries.
|
SegmentIntervalSolution
|
public final static int SegmentIntervalSolution = 4;
Sets this constant value to the type field
when the methods to receive segments as parameters store their intervalsolutions to this object.
Here, the methods to receive segments as parameters are the same as the case of the SegmentSolution.
|
SegmentHitInterval
|
public final static int SegmentHitInterval = 5;
Sets this constant value to the type field,
when this object is an output of the roughCheck method.
to receive segments as parameters store their intervalsolutions to this object.
|
TypeString
|
public final String[] TypeString
= {"Solution", "IntervalSolution","SegmentPtSolution","SegmentSolution",
"SegmentIntervalSolution ", "SegmentHitInterval"};
The String representations of type.
|
shapeIds
|
public String[] shapeIds=new String[2];
Sets the names of the ShapeContainers
which the parameters of the getNormalLinesBetweenShapes method:
curve1 and curve2 belong to.
Here the curve1 and curve2 are the objects of Curve2D abstract class.
|
curves
|
public Curve2D[] curves = new Curve2D[2];
Sets the parameters of getNormalLinesBetweenShapes method: curve1, curve2 objects.
Here the curve1 and curve2 are the objects of Curve2D abstract class.
|
t
|
public double[] t = new double[2];
Sets values to this field when the type=Solution or
SegmentSolution.
Here the t[0] and t[1] means the curve or segment parameters; t1 and t2
which the start or end point of the common normal line lies on.
And the curve1 and curve2 objects are stored in the curves[0] and curves[1]
which are the objects of Curve2D abstract class.
|
segments
|
public Segment2D[] segments = new Segment2D[2];
Sets the curve segments: segment1 and segment2 to this field when the type=
SegmentSolution,
SegmentIntervalSolution or
SegmentHitInterval.
Here the segment1 and segment2 are the objects of the Segment2D
|
depth
|
public int depth;
Sets a value to this field only when type=
SegmentHitInterval.
The depth is passed to the roughCheck method
and means a depth of the recursive call of the roughCheck method.
Sets the depth value to this field when the recursive call finishes.
This field is used for debug and reference.
|
numDiv
|
public int[] numDiv = new int[2];
Sets values to this field only when type=
SegmentHitInterval.
The numDiv is passed to the roughCheck method
and means the division number of the segments.
Sets the numDiv value to this field when the recursive call finishes.
This field is used for debug and reference.
|
divId
|
public int[] divId = new int[2];
Sets values to this field only when type=
SegmentHitInterval.
The divId is locally used in the roughCheck method
and represents the interval number of divided segments.
Sets the numDiv value to this field when the recursive call finishes.
This field is used for debug and reference.
|
interval
|
public double[] interval = new double[4];
Sets values to this field when the
type=IntervalSolution,
SegmentIntervalSolution or
SegmentHitInterval.
This field is used when a common normal line exists on some interval of the curves or
segments.
The t1=interval[0], t2=interval[1] represent the curve parameters of the curves[0] or
the segments[0], and
the t3=interval[2], t4=interval[3] represent the curve parameters of the curves[1] or
the segments[1].
|
boxSize
|
public double[] boxSize = new double[2];
Sets values to this field only when the type=
SegmentHitInterval.
The larger value between the width and height of the box covering the segments[0].
and the segments[1] respectively.
This field is used for debug and reference.
|
Method
|
Description
|
Constructor-1
|
public NormalsInfo(int type, String shapeId1, String shapeId2,
Curve2D curve1, Curve2D curve2, double t1, double t2)
The constructor for type=Solution.
|
Constructor-2
|
public NormalsInfo(int type, String shapeId1, String shapeId2,
Curve2D curve1, Curve2D curve2, double[] interval)
The constructor for type=IntervalSolution.
|
Constructor-3
|
public NormalsInfo(int type, Segment2D segment1, Segment2D segment2, double t1, double t2)
The constructor for type=SegmentSolution.
|
Constructor-4
|
public NormalsInfo(int type, Segment2D[] segments, double[] interval)
The constructor for type=SegmentIntervalSolution.
|
Constructor-5
|
public NormalsInfo(int type, Segment2D[] segments, int depth, int[] numDiv, int[] divId,
double[] interval, double[] boxSize)
The constructor for type=SegmentHitInterval.
|
getTypeString
|
public String getTypeString()
Returns the field variable: type
|
getBoxSize
|
public double[] getBoxSize()
Returns the field variable: boxSize.
|
getAngle
|
public double[] getAngle()
Stores the angle between the common normal line and the curves[0] to the double[0]
and stores the angle between the common normal line and the curves[1] to the double[1],
then return them.
If the common normal lines exist on the interval, then the angles are calculated at the mid point if the interval.
This method is used in the toString method .
|
getDistance
|
public double getDistance()
Calculates the length of the common normal line and returns it.
If the common normal lines exist on the interval, calculates the length at the mid point if the interval.
|
toString
|
public String toString()
Returns the string representing this object.
|
4. Class Vector2D
return=>page top
public class Vector2D
This class provides the 2D vector operations.
| Field |
Description |
x
|
double x
The x component of this vector.
|
y
|
double
The y component of this vector.
|
| Method |
Description |
Constructor
|
public Vector2D(double x, double y)
Sets the parameters to the corresponding fields.
|
Constructor
|
public Vector2D(Point2D point)
Sets the x, y components of the parameter to the corresponding fields.
|
getX
|
public double getX()
Return the x field.
|
getY
|
public double getY()
Return the y field.
|
setX
|
public void setX(double x)
Sets the parameter to the x field.
|
setY
|
public void setY(double y)
Sets the parameter to the y field.
|
toString
|
public String toString()
Returns the string representing this object.
|
clone
|
public Object clone()
Returns the clone object.
|
add
(static)
|
public static Vector2D add(Vector2D vec1, Vector2D vec2)
Returns (vec1+vec2).
|
sub
(static)
|
public static Vector2D sub(Vector2D vec1, Vector2D vec2)
Returns (vec1-vec2).
|
sub
(static)
|
public static Vector2D sub(Point2D p1, Point2D p2)
Returns the Vector2D object of (p1-p2).
|
multiply
(static)
|
public static Vector2D multiply(double scalar, Vector2D vec)
Returns (scalar*vec).
|
sproduct
(static)
|
public static double sproduct(Vector2D vec1, Vector2D vec2)
Returns the scalar product of vec1 and vec2.
|
vproduct
(static)
|
public static double vproduct(Vector2D vec1, Vector2D vec2)
Returns the vector product of vec1 and vec2.
 : the vector product=vec1.getX()*vec2.getY()-vec1.getY()*vec2.getX() : the vector product=vec1.getX()*vec2.getY()-vec1.getY()*vec2.getX()
|
isSameDirection
(static)
|
public static boolean isSameDirection(Vector2D vec1, Vector2D vec2, double
tolerance)
Returns true if the angle between vec1 and vec2 is smaller than the
tolerance.
The tolerance should be given as degree.
|
unitVector
(static)
|
public static Vector2D unitVector(Vector2D vec)
Returns the unit vector of vec.
|
normalVector
(static)
|
public static Vector2D normalVector(Vector2D vec)
Returns the normal vector of vec.
|
unitNormalVector
(static)
|
public static Vector2D unitNormalVector(Vector2D vec)
Returns the unit normal vector of vec.
|
project
(static)
|
public static Vector2D project(Vector2D vec1, Vector2D vec2)
Returns the vector which length is equal to the length of vec1 and which
direction is equals to the direction of vec2
|
length
(static)
|
public static double length(Vector2D vec)
Returns the length of vec.
|
dist
(static)
|
public static double dist(Vector2D vec1, Vector2D vec2)
vec2-vec1の長さを返す.
Returns the length of (vec2-vec1).
|
dist
(static)
|
public static double dist(Point2D p1, Point2D p2)
Returns the distance between p1 and p2.
|
crossPoint
(static)
|
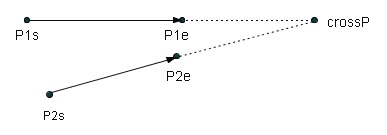
public static CrossCurvePT crossPoint(Point2D p1s, Point2D p1e, Point2D p2s, Point2D p2e)
Sets the crossP to the CrossCurvePT object and returns it.
|
5. Class Matrix2D
return=>page top
public class Matrix2D
This class provide the 2D matrix operations. A 2D matrix is represented as follow.

| Field |
Description |
matrix
|
double[][] matrix
The array of 3*3 which stores the matrix elements.
|
| Method |
Description |
Constructor
|
public Matrix2D()
Creates a new Matrix2D object of unit matrix.
|
Constructor
|
public Matrix2D(double[] elm)
Creates a new Matrix2D object which elements are by the parameter.
The length of the array of the elm is six and the matrix element of m00,
m10, m01, m11, m02 and m12 are stored in the elm in order.
|
getElm
|
public double[][] getElm()
Returns the matrix field.
|
getElm
|
public double getElm(int i, int j)
Returns the i, j-element of the matrix field.
|
setElm
|
public void setElm(int i, int j, double elm)
Sets the elm t the i, j-element of the matrix field.
|
addElm
|
public void addElm(int i, int j, double add)
Adds the elm t the i, j-element of the matrix field.
|
getAffineTransform
|
public AffineTransform getAffineTransform()
Returns the java.awt.geom.AffineTransform object using the m00, m10,
m01, m11, m02 and m12 elements of this object.
|
setAffineTransform
|
public void setAffineTransform(AffineTransform affine)
Sets the parameter of the affine to this object.
|
toString
|
public String toString()
Returns the string representing this object.
|
transForm
(static)
|
public static Vector2D transForm(Matrix2D M, Vector2D vec)
Returns the transformed vector from vec by matrix M.
|
transForm
(static)
|
public static Point2D transForm(Matrix2D M, Point2D p)
Returns the transformed point from p by matrix M.
|
scalarMult
(static)
|
public static Matrix2D scalarMult(double mult, Matrix2D M)
Returns the matrix scaling with the specified mult amount.
|
multMatrix
(static)
|
public static Matrix2D multMatrix(Matrix2D M1, Matrix2D M2)
Returns the multiplied matrix of the two matrices of M1
and M2.
|
InverseMatrix
(static)
|
public static Matrix2D InverseMatrix(Matrix2D M)
Returns the inverse matrix of M.
|
getScaleMatrix
(static)
|
public static Matrix2D getScaleMatrix(double scale)
Returns the scaling matrix.
|
getResizeMatrix
(static)
|
public static Matrix2D getResizeMatrix(Rectangle2D oldBox, Rectangle2D
newBox)
Returns the matrix which transforms oldBox to newBox.
|
getRotationMatrix
(static)
|
public static Matrix2D getRotationMatrix(Point2D anchorP, Vector2D vec1,
Vector2D vec2)
Returns the rotation matrix with scaling which transforms the
vector of (vec1-anchor) to the vector of (vec2-anchor).
|
getFlipMatrix
(static)
|
public static Matrix2D getFlipMatrix(int direction, double value)
Returns the flipping matrix (mirror transformation matrix). If direction
equals 0, then returns the matrix for flipping horizontally, otherwise
returns the matrix for flipping vertically.
|
multMatrix
(static)
|
public static AffineTransform multMatrix(AffineTransform M1, AffineTransform
M2)
Returns the multiplied affine transformation matrix by the two affine transformation
matrices of M1 and M2.
|
print
(static)
|
public static void print(Matrix2D M)
Print the matrix of M.
|
6. Class Matrix
return=>page top
public class Matrix
Currently, this class is used for creating a spline curve.
 =>FergusonCurve2D.createNaturalSpline =>FergusonCurve2D.createNaturalSpline
| Field |
Description |
eps
|
static double eps=1e-12
The very small number.
|
| Method |
Description |
GaussianElimination
(static)
|
public static double[] GaussianElimination(double[][] A0, double[] b0)
Solves the linear equation of A0*x=b0 by the Gaussian elimination and returns
the solution vector x.
The matrix A0 and the vector b are not changed.
|
InverseMatrix
(static)
|
public static double[][] InverseMatrix(double[][] A)
Returns the inverse matrix of A by using the Gaussian elimination.
|
multMatrix
(static)
|
public static double[][] multMatrix(double[][] A, double[][] B)
Returns the multiplied matrix of the two matrices of M1
and M2.
|
print
(static)
|
public static void print(double[][] A, double[] b, double[] x)
Prints the A, b, x of the equation A*x=b, and the residue.
|
|
![]()
![]()
![]()
![]()
 =>
DrawTest: Intersection between two arbitrary curves ,
Normal lines to a arbitrary curve
=>
DrawTest: Intersection between two arbitrary curves ,
Normal lines to a arbitrary curve  =>
The formulas of the Newton-Raphson method for intersection.
=>
The formulas of the Newton-Raphson method for intersection.
 : The formulas of the Newton-Raphson method for intersection.
return=>Intersection points between two curves
: The formulas of the Newton-Raphson method for intersection.
return=>Intersection points between two curves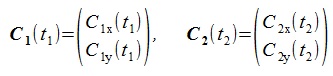
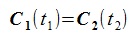
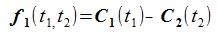
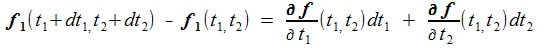 (1)
(1)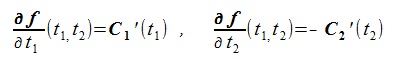
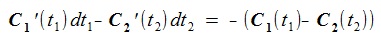
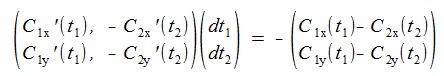 (2)
(2) =>
The formulas of the Newton-Raphson method for normal lines
=>
The formulas of the Newton-Raphson method for normal lines
 :
The formulas of the Newton-Raphson method for normal lines
return=>Normal lines to a curve from a point
:
The formulas of the Newton-Raphson method for normal lines
return=>Normal lines to a curve from a point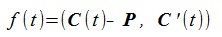 (x,y): scalar product,
P: the given point, C'(t): derivative
(3)
(x,y): scalar product,
P: the given point, C'(t): derivative
(3)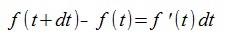
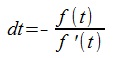 (4)
(4)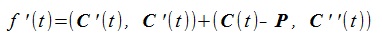 (5)
(5) =>
Processing Method
=>
Processing Method : Processing Method
return=>Common normals between two shapes
: Processing Method
return=>Common normals between two shapes :
In the normal coordinate, e1×e2≧0 is satisfied
if the rotation from e1 to e2 is counter clockwise,
however in the graphic coordinate, the outer product≧0 is satisfied if the rotation is clockwise,
because the y-axis is downward.
:
In the normal coordinate, e1×e2≧0 is satisfied
if the rotation from e1 to e2 is counter clockwise,
however in the graphic coordinate, the outer product≧0 is satisfied if the rotation is clockwise,
because the y-axis is downward. => The test results are shown in
Java Drawing Test Codes Figure 3.1, 3.2.
=> The test results are shown in
Java Drawing Test Codes Figure 3.1, 3.2.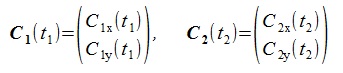 (1)
(1)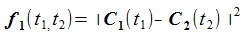 (2)
(2) (3)
(3)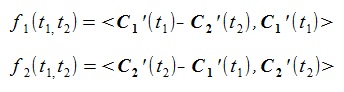 (4)
(4)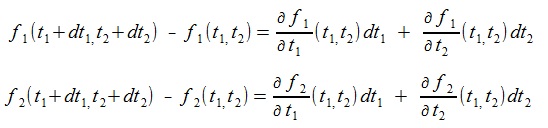 (5)
(5)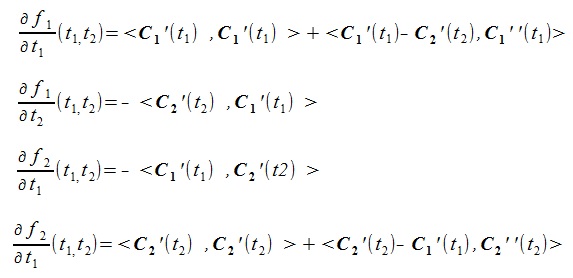 (6)
(6)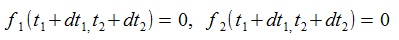 (7)
(7)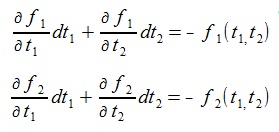 (8)
(8)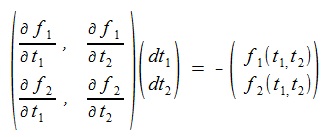 (9)
(9)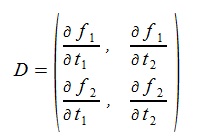 (10)
(10)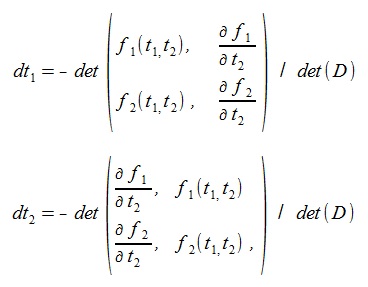 (11)
(11) =>FergusonCurve2D.createNaturalSpline
=>FergusonCurve2D.createNaturalSpline