 |
2曲線への共通垂線の計算 2016.10.20 |
|
||||||
ホーム
| Ref.=> |
トピックスInput Method Frameworkによる |
Chapter: 1. ソースコードダウンロード, 2. 処理方法, 3. テスト結果, 4. Test code,
=> NormalLinesBetweenShapesBasic.zip, NormalLinesBetweenShapes.zip
2. 処理方法戻る=>page top
2.1 処理ステップ(図2.1, 2.2)
ステップ1. 共通垂線の存在可能性の判定
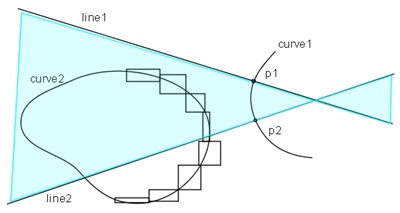
図2.1に示すように曲線curve1を細かく分割して、分割区間に変曲点(inflection point)を持たないようにする。 分割区間の両端p1、p2でcurve1の垂線line1, line2を作成する。 一方、曲線curve2も細かく分割し、分割区間を矩形で覆う(被覆矩形: bounding box)。
このとき、curve2の被覆矩形の一部または全部が、line1, line2に挟まれた領域（水色の領域）内にあれば、 その被覆矩形内部のcurve2分割区間と、curve1の分割区間(p1, p2区間)には共通垂線が存在する可能性があると判定できる。
またこのようにして見つけたcurve2の分割区間に対して垂線line1, line2を作成し、 curve1の分割区間を被覆矩形で覆って、前記と同様な判定処理を行い、 共通垂線があり得ると判定されれば、共通垂線の存在可能性はより高くなる（図3.2)。
ステップ2. 二分法による高精度化
ステップ1の方法で共通垂線があり得ると判定されたcurve1, curve2の分割区間を、2分法で分割し、 ステップ1と同様な判定処理を行い、共通垂線の存在する分割区間の範囲を狭める。
この処理は分割区間が十分に小さくなるまで、再帰呼び出しで処理する。
ステップ3. Newton Raphson法による高精度計算
ステップ2で十分に小さくなった分割区間の中央点を初期値としてNewton Raphson法を実行する。
 |
 |
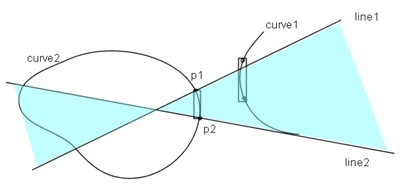| 図2.1 共通垂線の存在可能性の判定(1) | 図2.2 共通垂線の存在可能性の判定(2) |
2.2 計算式戻る=>page top
2.2.1 上記Step1の計算式 (図2.3(a)-(e))
被覆矩形の一部または全体が2直線(line1, line2)に挟まれた領域にあるか否かを判定するには、 被覆矩形の頂点が、その領域にあるか否かを判定できれば良い。 下記(a)-(d)は、line1, line2が並行でない場合、(e)は平行な場合について述べる。
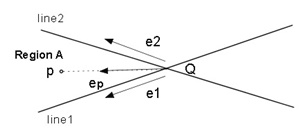
図2.3(a)に示すように。line1, line2方向の単位ベクトルをe1, e2 とし、line1, line2の 交点Qからpへ向かう単位ベクトルをep とする。点pが領域A(Region A)に存在するための条件を求める。 e1, e2 , ep は2次元ベクトルであるが3次元ベクトルと見なし、 ベクトルの外積のz値を2次元ベクトルの外積値(スカラー)として扱う。
e1×e2 =e1x * e2y - e1y * e2x(1)
e1×e2 はe1とe2 が作る平行四辺形の符号つき面積である。 ここではe1×e2 ≧0と仮定する(e1×e2<0ならばe11とe2 を交換する)。
(a) pが領域Aにあるための条件はつぎの式が成立することである(図2.3(a))
0≦e1×ep ≦e1×e2 かつ0≦ep×e2 ≦e1×e2(2)
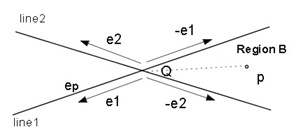
(b)pが領域Bにあるための条件(図2.3(b))
0≦(-e1)×ep≦(-e1)×(-e2) かつ0≦ep×(-e2)≦(-e1)×(-e2)
=> -(e1×e2)≦e1×ep≦0 かつ-(e1×e2)≦ep×e2≦0(3)
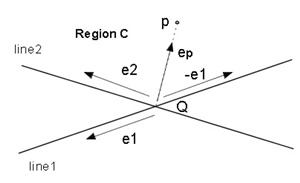
(c) pが領域Cにあるための条件(図3.3(c))
0≦ep×(-e1)≦e2×(-e1)かつ0≦e2×ep≦e2×(-e1)
=> 0≦e1×ep≦e1×e2かつ0≦-(ep×e2)≦e1×e2
=> 0≦e1×ep≦e1×e2 かつ-(e1×e2)≦ep×e2≦0(4)
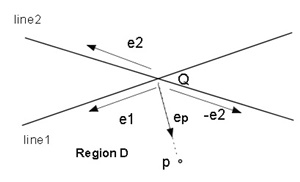
(d) pが領域Dにあるための条件(図2.3(d))
0≦ep×e1≦(-e2)×e1かつ0≦(-e2)×ep≦(-e2)×e1
=> 0≦-(e1×ep)≦e1×e2かつ0≦ep×e2≦e1×e2
=> -(e1×e2)≦e1×ep≦0 かつ0 ≦ep×e2≦e1×e2(5)
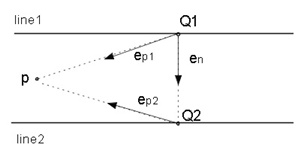
(e) pがline1, line2の間の領域あるための条件(図2.3(e))
図2.3(e)にあるように単位ベクトルを定義すると、条件はつぎ。
0≦en×ep1≦|Q2-Q1| (6)
ここで|Q2-Q1|はline1, line2間の距離。
(注)実際のテスト結果を下の図3.1, 3.2に示す。
 (a) |
 (b) |
 (c) |
 (d) |
 (e) |
|
| 図2.3 ステップ1の計算式 | |
2.2.2 上記ステップ3のNewton Raphson法の計算式戻る=>page top
曲線パラメータをt1, t2、曲線C1, C2のx,y成分を縦ベクトル表示で次のように表す(太文字はベクトル)。
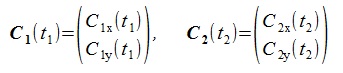(1)共通垂線を求めるには、2曲線間の距離(次式)をローカルに最小化(Local Minimum)にするt1, t2を求めればよい。
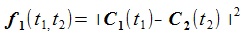(2)最小化するには次の条件が必要である(
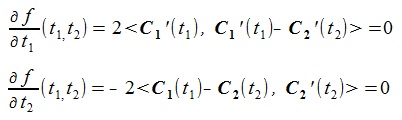(3)上式の右辺をf1(t1,t2）、f2(t1,t2） と書く。
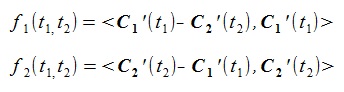(4)dt1, dt2 を無限小とすれば(教科書ではΔt1, Δt2 と書く)、 f1(t1,t2)、f2(t1,t2) に対しては全微分、偏微分の関係から次式が成立。
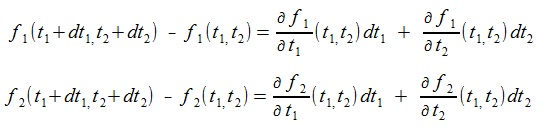(5)ここで、(5)式右辺の偏微分は次式で与えられる。
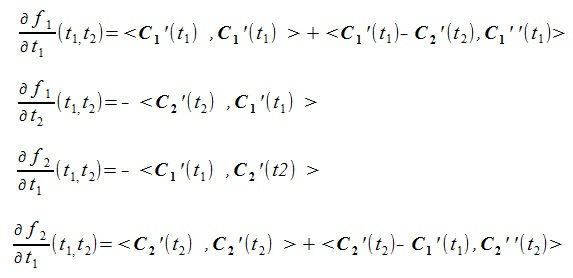(6)NewTon-Raphson法の近似式は、次のように(5)式の左辺の項を0と置いて求める。
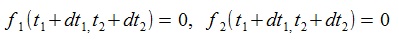(7)(5)式は次のようになる。
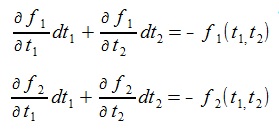(8)(8)式マトリックを使い、次のように書ける。
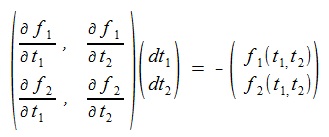(9)これを解けば、dt1, dt2 は次のように求まる(detはdeterminant)
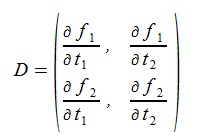(10)ここでDは次のマトリックス。
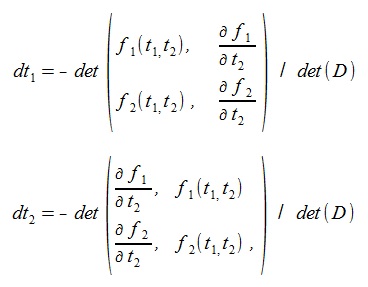(11)3. テスト結果戻る=>page top
3.1 テスト コード: NormalLinesBetweenShapesBasic
|
|
|
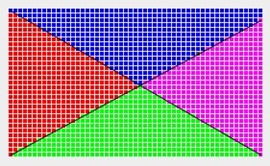
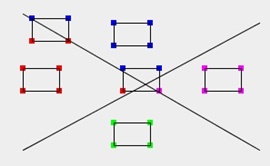
| 図3.1(a) ステップ1の計算式(図2.3(a)-(d)) |
図3.1(b) ステップ1の計算式(図2.3(e)) |
図3.1(c) 同左: 被覆矩形の頂点ごとに表示 |
| 格子点ごとにステップ1の判定を行い結果を色で表示 | ||
|
|
|
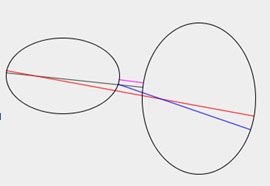
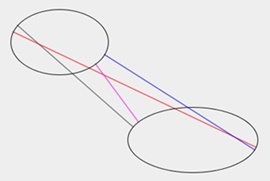
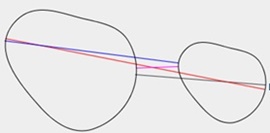
| 図3.2(a) 楕円vs.楕円 | 図3.2(b) 楕円vs.楕円 | 図3.2(c) スプラインvs.スプライン |
| 複数の共通垂線を見やすく色分けで表示 | ||
3.2 テスト コード: NormalLinesBetweenShapes
|
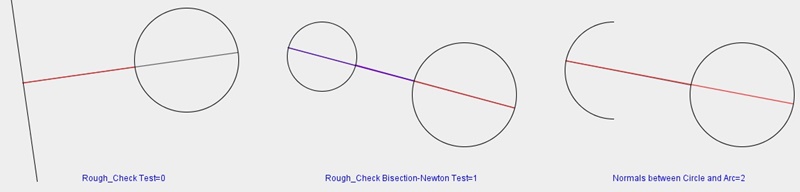
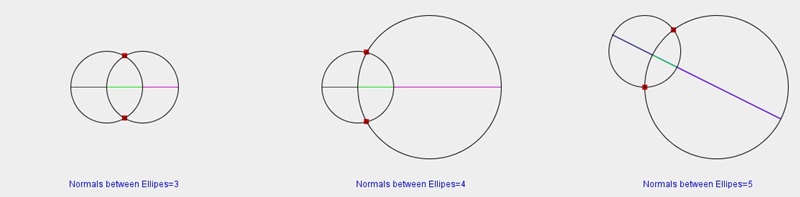
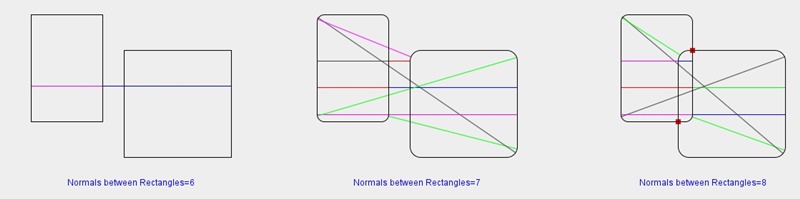
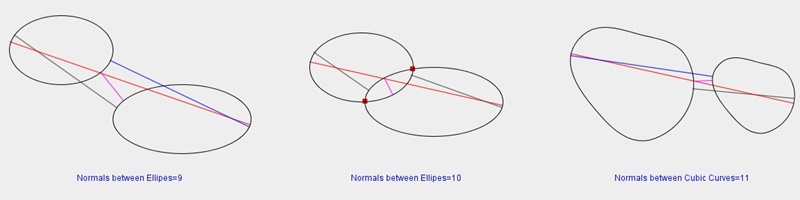
図3.3 様々な共通垂線の計算(赤丸は交点) |
4. Test code戻る=>page top
NormalLinesBetweenShapesとNormalLinesBetweenShapesBasicのコードは同じ。TestCaseの設定が異なるだけ。
4.1 クラス一覧
|
クラス |
説明 |
|
NormalLinesBetweenShapes |
public class ormalLinesBetweenShapes extends JFrame Jframe, JScrollPane, JViewport, Panelオブジェクトを作成し組み立てる。 |
| NormalLinesBetweenShapesPanel |
public class ormalLinesBetweenShapesPanel extends JPanel このオブジェクトの上に図1の図形と交点を描画する。 |
| TestCase |
public class TestCase
=> TestCase of the RegionHitTest.
|
| TestCurve |
public class TestCurve
=> TestCurve of the RegionHitTest.
|
| パラメトリック曲線 |
Segment2D,
Curve2D,
Rectangle2DE,
RoundRectangle2DE,
Ellipse2DE,
Line2DE,
Polyline2DE, CubicCurve2DE, GeneralCurve2DE, FergusonCurve2D |
| 幾何計算ライブラリ |
Curve2DUtil.getNormalLinesBetweenShapes,
Curve2DUtil.NormalsInfoサブクラス, CrossCurvePT, Matrix, Matrix2D |
4.2 クラス仕様
4.2.1 public class NormalLinesBetweenShapesPanel extends JPanel
|
メソッド |
説明 |
| createTestCase |
public void createTestCase() TestCaseオブジェクトを作成する。 |
| getGridPoints |
public Point2D[] getGridPoints(Rectangle2D box) 引数: box - Rectangle2D オブジェクト。 box内部に生成した格子点。 処理: 引数で指定したRectangle2D オブジェクトの内部に格子点を生成して返す。 |
| paint |
public void paint(Graphics g) 処理: このクラス(NormalLinesBetweenShapesPanel)のオブジェクトに図形と共通垂線を描画する。 paintPtRegion, paintRectRegion, paintSolutionを呼び出す。 |
| paintPtRegion |
public void paintPtRegion(Graphics g, TestCase testCase) 処理: =>
図3.1(a), 図3.1(b)計算式=> 2.2.1 上記Step1の計算式 |
| paintRectRegion |
public void paintRectRegion(Graphics g, TestCase testCase) 処理: =>
図3.1(c)被覆矩形の4頂点の領域コードをpaintPtRegionで取得し描画する。 |
| paintSolution |
public void paintSolution(Graphics g, TestCase testCase) 処理: =>
図3.2, 図3.3Curve2DUtil.getNormalLinesBetweenShapes メソッドにより2図形の共通垂線を計算し描画する。 |
All other trademarks are property of their respective owners.