|
Summary:The parametric curve representation is useful for geometric calculation such as
calculating intersection points of two curves etc. We extends the classes
of the Rectangle2D, RoundRectangle2D, Ellipse2D and so on in java.awt.geom
to be able to handle a parametric curve.
|
|
Relevant major classes of Java SE: java.awt.*, java.geom.*
|
|
Classes on this page: Segment2D,
geomExtension, Curve2D,
Rectangle2DE, RoundRectangle2DE,
Ellipse2DE, Line2DE,
Polyline2DE, CubicCurve2DE,
GeneralCurve2DE, FergusonCurve2D |
1. Overview of the parametric curve
1.1 The definition
A two dimensional parametric curve is defined by a parameter t and two
functions (Cx(t), Cy(t)) which give the (x,y) coordinates for parameter
t. We denote the parametric curve as follow.
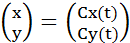 (1) (1)
The Cx(t) and Cy(t) are usually expressed by a piecewise function.
Each piece is a polynominal function, circular functions and so on.
For example, the bondary curve of the java.awt.geom. RoundRectangle2D consists of eight pieces - four
straight lines and four arcs of the 90° central angle -
and those pieces are arranged as line->arc->line->arc->⋅ ⋅
⋅ ⋅ ⋅ ⋅ ⋅ ⋅ .
We defines the domain (interval) of the curve parameter t for each
piece as 0≤t≤1 for the first piece, 1≤t≤2 for the second piece and so on.
Hereafter we call each piece as a curve segment or a segment and the junction point of two pieces as a segment junction point.
Let's denote the number of the curve segments of a parametric curve as
nseg, then the curve segments numbered as 0,1,2⋅ ⋅ ⋅ ,nseg-1, and
the segment junction points are numbered as 0,1,2⋅ ⋅ ⋅ ,nseg.
1.2 The expressions of parametric curve segment
(1) Elliptic arc (circular arc)
The elliptic arc corresponds to the java.awt.geom.Arc2D and its parametric
curve ie expressed as follow
Cx(t)= a*cos((θextent*t+θstart)*π/180)+x0 (2)
Cy(t)= - b*sin((θextent*t+θstart)*π/180)+y0
The plus direction of the y-axis on the screen is downward, so a minus sign is needed
for the expression of the Cy(t).
Here, (a) the angles are represented in degrees, (b) the plus rotation of the angle is anticlockwise.
And the notations in the (2) are as follow.
⋅ (x0,y0): The center of the arc.
⋅ a, b: the The transverse diameter and conjugate diameter.
⋅ θextent: The angular extent of the arc in degrees.
⋅ θstart: The starting angle of the arc in degrees.
⋅ π: The circle ratio.
(2) CubicCurve(Bezier curve segment)
P(t)=(1-t)3 Q0 + 3(1-t)2t
Q1 + 3(1-t)t2 Q2 + t3Q3 (A bold character represents a vector)
(3)
The Bezier curve segment consists of four points. The Q0, Q3 are
the endpoints of the segment, and Q1, Q2 are
the control points which the segment doesn't generally pass through.
Table 1 Blending functions
|
|
X0(t)
|
X1(t)
|
X2(t)
|
X3(t)
|
|
Xi(t)
|
(1-t)3
|
3(1-t)2t
|
3(1-t)t2
|
t3
|
|
First derivatives: Xi'(t)
|
-3(1-t)2
|
3(1-t)(1-3t)
|
3(2-3t)t
|
3t2
|
|
Second derivatives: Xi''(t)
|
6(1-t)
|
-6(2-3t)
|
6(1-3t)
|
6t
|
Table 2 The function and the derivatives at t=0, 1
|
|
t=0
|
t=1
|
|
P(t)
|
Q0
|
Q3
|
|
First derivatives: P'(t)
|
-3Q0+3Q1 |
-3Q2+3Q3
|
|
Second derivatives: P''(t)
|
6Q0-12Q1+6Q2
=6(Q2-Q1)- 6(Q1-Q0)
|
6Q1-12Q2+6Q3
=6(Q3-Q2)- 6(Q2-Q1)
|
(3) Ferguson curve segment
The Bezier curve can be rewritten as follows:
P(t)= X0(t)Q0 + X1(t)Q1 + X2(t)Q2 + X3(t)Q3
= (X0(t)+X1(t))Q0 + X1(t)(Q1 - Q0 ) - X2(t)(Q3 - Q2 ) + (X2(t)+X3(t))Q3
= (X0(t)+X1(t))P(0) + (X2(t)+X3(t)) P(1) + X1(t)/3 P'(0) - X2(t)/3 P'(1)
= f0(t) P0 + f1(t)P1 + g0(t) T0 - g1(t)T1
(4)
The last formula is the expression of the Ferguson curve segment.
Here, P0= P(0),
P1= P(1), T0= P'(0),
T1= P'(1)
 =>
Figure 1.1 (a) =>
Figure 1.1 (a)
and the functions of f0(t), f1(t),
g0(t) and g1(t) are expressed as Table 3.
Table 3 Ferguson blending functions
|
|
f0(t)
= X0(t)+ X1(t))
|
f1(t)
= X2(t)+X3(t)
|
g0(t)
= X1(t)/3
|
g1(t)
= X2(t)/3
|
|
fi(t), gi(t)
|
(1-t)2(1+2t)
|
(3-2t)t2
|
(1-t)2t
|
(1-t)t2
|
|
First derivatives: fi'(t), gi'(t)
|
-6(1-t)t
|
6(1-t)t
|
(1-t)(1-3t)
|
(2-3t)t
|
|
Second derivatives: fi''(t), gi''(t)
|
-6+12t
|
6-12t
|
-4+6t
|
2-6t
|
The relation of the functions:
f0(t)= f1(1-t), f0(1-t)= f1(t),
g0(t)= g1(1-t), g0(1-t)= g1(t)
The expression of (4) may be convenient for handling the tangent vectors
of the curve segment because the tangent vectors are expressed explicitly.
The definition of Tin, Tout
A spline curve can be represented by multiple Ferguson segments. In this
case, two tangent vectors are defined at the i-th segment junction point - the first
tangent vector is used for interpolate the (i-1)-the segment and the second
is for the i-th segment. Those tangent vectors are denoted by P'(1)
and P'(0) in the (4) and hereafter those vectors are denoted by Tin[i] and Tout[i]
respectively.
In the case of a smooth spline, the directions of Tin[i] and Tout[i] are
the same, however the lengths of Tin[i] and Tout[i] are not equal in general.
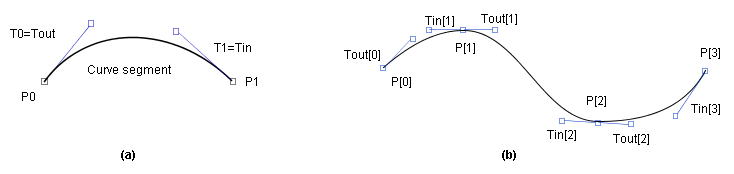
Figure 1.1 Curve segment and Tin, Tout
Annotation: The real (mathematical) direction of the Tin is the inverted direction
that the Figure shows.
2. Class Segment2D
return=>page top
public class Segment2D
The Segment2D class represents a parametric curve segment of Line2D,
Arc2D and CubicCurve2D in the java.awt.geom package. The QuadCurve2D
in the java.awt.geom is not used for the parametric curve segment, because
it doesn't seem useful.
The major function of the Segment2D class is to calculate the position,
tangent vector and second derivative vector of the parametric curve segment
for a given parameter t (0≤t≤1) by
the expression of the parametric curve segment.
| Field |
Description |
|
type
|
int type
This field represents the type of the parametric curve segment.
One of the LINE, ARC or CUBIC is set to this filed.
|
| shape |
private Shape shape
One of the Line2D, Arc2D or CubicCurve2D object in the java.awt.geom
is set to this field according to the type.
|
|
affineTransform
|
private AffineTransform affineTransform
Stores the AffineTransform for the Arc2D object.
If the type equals Line or CUBIC, this field is not used to represent a transformed
object, because the transformed object can be created from the original
Line2D or CubicCurve2D object by transforming is endpoints and control points.
|
|
MOVETO
|
public static final int MOVETO=0
The constants to be set to the type field.
Moves a point to the start point of the next subpath.
|
|
LINE
|
public static final int LINE=1
The constants to be set to the type field.
The Line2D object is set to the shape field.
|
|
ARC
|
public static final int ARC=2
The constants to be set to the type field.
The Arc2D object is set to the shape field.
|
|
CUBIC
|
public static final int CUBIC=3
The constants to be set to the type field.
The CubicCurve2D object is set to the shape field.
|
|
QUAD
|
public static final int QUAD=4
The constants to be set to the type field.
The QuadCurve2D object is set to the shape field.
Not used currently.
|
| Method |
Description |
|
Constructor
|
public Segment2D(int type, Shape shape)
Sets the parameters to the corresponding field.
Null is set to the affineTransform field.
|
|
Constructor
|
public Segment2D(int type, Shape shape, AffineTransform affineTransform)
Sets the parameters to the corresponding field.
|
|
getType
|
public int getType2()
Returns the type field.
|
| isAffineTransform |
public boolean isAffineTransform()
Return true if the affineTransform isn't null.
|
|
getShape
|
public Shape getShape()
Returns the shape field.
If thetype equals ARC and the
affineTransform isn't null,
then return the java.awt.geom.GeneralPath object which is created by using the
shape and the affineTransform.
 =>
Returning the transformed Arc2D =>
Returning the transformed Arc2D
|
|
getP
|
public Point2D getP(double t)
Parameter:
t - The parameter of the curve segment.. 0≤t≤1.
Returns:
The position (x,y) of the curve segment at the parameter t.
|
|
getTangent
|
public Vector2D getTangent(double t)
Parameter:
t - The parameter of the curve segment. 0≤t≤1.
Returns:
The derivative (tangent vector) of the curve segment at the parameter t.
|
|
getTangentDerivative
|
public Vector2D getTangentDerivative(double t)
Parameter:
t - The parameter of the curve segment. 0≤t≤1.
Returns:
The second derivative (vector) of the curve segment t at the parameter t.
|
| getEndPoints |
public Point2D[] getEndPoints()
Returns the endPoints of this object. |
| getCharacteristicPoints |
public CurvePT[] getCharacteristicPoints()
Returns the characteristic points of this object. Characteristic points
are endpoints and middle points of the curve segments of this object, and
north, south, east and west points of an ellipse or a circle. |
|
getSegmentLength
|
public double getSegmentLength(double t1, double t2)
Returns the curve length of the curve segment interval (t1≤t≤t2). 0≤t1, t2≤1.
|
|
getBoundingBox
|
public Rectangle2D getBoundingBox()
Returns the bounding box enclosing the curve segment.
|
|
getBoundingBox
|
public Rectangle2D getBoundingBox(double t1, double t2)
Returns the bounding box enclosing the curve segment interval (t1≤t≤t2).
0≤t1, t2≤1
|
|
resizeSegment
|
public Segment2D resizeSegment(Rectangle2D oldBox, Rectangle2D newBox)
Parameters:
oldBox - The previous dragged rectangle.
newBox - The current dragged rectangle.
Returns:
The resized Segment2D object.
Processing:
⋅ If the affineTransform equals null,
then performs the following.
Creates the resized Line2D, Arc2D or CubicCurve2D objects and creates
a new Segment2D object using the type and the resized object.
⋅ If the type equals ARC and the
affineTransform doesn't equals null,
then performs the following.
Creates a transforming matrix by the
getResizeMatrix method of the
Matrix2D.
And calculates the multiplied matrix by the affineTransform
and the transforming matrix, then returns a new Segment2D object
which is created by using the type,
the shape and the multiplied matrix.
|
|
trimSegment
|
public Segment2D trimSegment(double t1, double t2)
Parameters:
t1 - The start parameter of the trimmed segment.
t2 - The end parameter of the trimmed segment.
0≤t1, t2≤1
Returns:
The trimmed Segment2D object.
Processing:
Creates the trimmed Shape object of Line2D, Arc2D or CubicCurve2D.
Then creates a new Segment2D object using the
type, the trimmed Shape and the
affineTransform, and returns the new Segment2D.
|
|
getFergusonCurve
|
public FergusonCurve2D getFergusonCurve()
Returns:
The FergusonCurve2D object converted from this Segment2D object.
Processing:
⋅ If the type equals LINE or CUBIC, then performs the following.
In this case, the Segment2D object can be converted to a single Ferguson
segment within round-off error. So, returns the FergusonCurve2D of single segment.
⋅ If the type equals ARC, then performs the following.
The Segment2D can be approximated with multiple Ferguson segments by using
the getOptimizedTangents method of the FergusonCurve2D. The number of the Ferguson segments is determined so that the approximation error
is lower than 1e-8 for a unit circle.
As the result, the error range can be lower than 1e-4 for any shape
on the canvas. In this case, returns the FergusonCurve2D of multiple segments.
|
|
transformSegment
|
public Segment2D transformSegment(Matrix2D M)
Parameters:
M - The transforming matrix.
Returns:
The transformed Segment2D object.
Processing:
⋅ If the type equals Line2D or CubicCurve2D, then performs the following.
Creates a new Line2D or CubicCurve2D object by transforming the endpoints
and control points of the shape
and creates a new Segment2D object using the type
and the new Line2D or CubicCurve2D object.
⋅ If the type equals ARC, then performs the following.
Calculates the multiplied matrix of the affineTransform
and the transforming matrix M and created a new Segment2D object by using the
type, the shape and the multiplied matrix.
Then returns the new Segment2D object.
|
|
reverseSegment
|
public Segment2D reverseSegment()
Returns:
The Segment2D object which is reversed in curve direction.
Processing:
Creates a new Line2D, Arc2D or CubicCurve2D object whose direction is reversed
and creates a new Segment2D object using the type
and the reversed object, then returns the new Segment2D object.
|
| moveSegmentEndPT |
public Segment2D moveSegmentEndPT(int index, Point2D newPT)
Parameters:
index - if the index equals 0, then move the start point of the curve segment,
otherwise moves the end point of the curve segment.
newPT - The new endpoint.
Returns:
The Segment2D object whose specified endpoint was moved to the newPT.
Processing:
⋅ The case of the type equals LINE
Replaces the specified endpoint by the newPT.
⋅ The case of the type equals ARC
Creates the transforming matrix by the
getRotationMatrix method of the
Matrix2D
and transforms this Segment2D object by the
transformSegment method.
⋅ The case of the type equals CUBIC
Creates a new segment2D object by using the
movePoint method of the
FergusonCurve2D.
|
| moveSegmentTangent |
public void moveSegmentTangent(int index, Vector2D newTangent)
Parameters:
index - if the index equals 0, then changes the tangent line at the start point,
otherwise changes the tangent line at the end point of the curve segment.
newtangent - The new tangent vector.
Returns:
The Segment2D object whose direction of the tangent line at the specified
endpoint was changed to the the direction of the newTangent.
Processing:
This method is used only for the Segment2D object whose type equals CUBIC.
Creates a new segment2D object by using the moveTangent method
of the FergusonCurve2D.
|
|
clone
|
public Object clone()
returns the clone of this object.
|
|
toString
|
public String toString()
Returns the string representing this object.
|
|
getSerializableSegment2D
|
public SerializableSegment2D getSerializableSegment2D()
Returns the SerializableSegment2D object
which is used for writing this object to the file.
|
 :
Returning the transformed Arc2D :
Returning the transformed Arc2D
Shape shape=this.shape;
if(this.type==ARC&&this.affineTransform!=null){
GeneralPath generalpath=new GeneralPath();
generalpath.append(shape, false);
generalpath.transform(this.affineTransform);
shape=generalpath;
}
return shape;
3. The extension of java.awt.geom (geomExtension)
return=>page top
We extends the classes of the Rectangle2D, RoundRectangle2D, Ellipse2D etc. in java.awt.geom
package to be able to handle a parametric curve. The names
of the extended classes are denoted by adding "E" at the end
of the original class names - Rectangle2DE, RoundRectangle2DE, Ellipse2DE etc.
The each extended class has the array of parametric curve segments (Segment2D objects) and the java.awt.Shape object.
The array of the parametric curve segments is used for calculating the
position (x,y), the tangent vector and the second derivative of the parametric
curve. The Shape object is used for drawing the shape of the parametric
curve by the methods of java.awt.Graphics and java.awt.Graphics2D. And
the Shape object is also used for testing whether a specified point
is inside the boundary of the Shape or not, by the contains method
of the Shape.
Creating the java.awt.Shape object of a parametric curve
The java.awt.geom.GeneralPath is employed to create the Shape object of
the parametric curve as follows.
Example:The constructor of the RoundRectangle2DE
A round rectangle consists of eight pieces of shapes - four
straight lines and four arcs of the 90° central angle -
and those pieces are arranged as line->arc->line->arc->⋅ ⋅
⋅ ⋅ ⋅ ⋅ ⋅ ⋅ as mentioned in 1.1.
public RoundRectangle2DE(double x, double y, double width, double height,
double arcw, double arch){
this.x=x; this.y=y; this.width=width; this.height=height;
this.arcw=arcw; this.arch=arch;
this.generalPath=new GeneralPath();
this.segments=new Segment2D[8];
Line2D line0=new Line2D.Double(x, y+0.5*arch, x, y+height-0.5*arch);
Line2D line1=new Line2D.Double(x+0.5*arcw, y+height, x+width-0.5*arcw, y+height);
Line2D line2=new Line2D.Double(x+width, y+height-0.5*arch, x+width, y+0.5*arch);
Line2D line3=new Line2D.Double(x+width-0.5*arcw, y, x+0.5*arcw, y);
Arc2D arc0=new Arc2D.Double(x, y+height-arch, arcw, arch, 180, 90, Arc2D.OPEN);
Arc2D arc1=new Arc2D.Double(x+width-arcw, y+height-arch, arcw, arch, 270,
90, Arc2D.OPEN);
Arc2D arc2=new Arc2D.Double(x+width-arcw, y, arcw, arch, 0, 90, Arc2D.OPEN);
Arc2D arc3=new Arc2D.Double(x, y, arcw, arch, 90, 90, Arc2D.OPEN);
segments[0]=new Segment2D(Segment2D.LINE, line0);
segments[1]=new Segment2D(Segment2D.ARC, arc0);
segments[2]=new Segment2D(Segment2D.LINE, line1);
segments[3]=new Segment2D(Segment2D.ARC, arc1);
segments[4]=new Segment2D(Segment2D.LINE, line2);
segments[5]=new Segment2D(Segment2D.ARC, arc2);
segments[6]=new Segment2D(Segment2D.LINE, line3);
segments[7]=new Segment2D(Segment2D.ARC, arc3);
for(int i=0;i<segments.length;i++){
Shape shape=segments[i].getShape();
generalPath.append(shape,true);
}
generalPath.closePath();
}
4. abstract class Curve2D
return=>page top
public abstract class Curve2D
This class provides basic and common methods of the parametric curve. The
other classes are the extended classes of this abstract class.
| Field |
Description |
|
segments
|
Segment2D[] segments
The Segment2D objects which compose this parametric curve.
|
|
generalPath
|
GeneralPath generalPath
The GeneralPath object which is referred as java.awt.Shape in getShape method..
This object is created by appending the shape - Line2D, Arc2D or CubicCurve2D - of
Segment2D objects in the Curve2D constructor.
 =>
Creating and extracting java.awt.Shape =>
Creating and extracting java.awt.Shape
|
|
closed
|
boolean closed
True if this parametric curve is closed.
|
|
Constants which represent Curve2D extensions
|
public static final int RECTANGLE=1, ROUND_RECTANGLE=2, ELLIPSE=3, LINE=4,
POLYLINE=5, CUBIC_CURVE=6, GENERAL_CURVE=7
The constants representing the type of the extended classes of this class.
|
|
eps
|
public final static double eps=1e-5
The small number.
|
| largeNumber |
public final static double largeNumber=1e+5
The large number. |
| ClosedTolerance |
public final static double ClosedTolerance=3d
The number used for testing whether the parametric curve is closed
or not. |
| Method |
Description |
|
Constructor
|
public Curve2D(Segment2D[] segments)
Create a new Curve2D object with the Segment2D objects.
this.segments=segments;
this.generalPath=new GeneralPath();
Point2D startP=segments[0].getP(0);
Point2D endP=segments[segments.length-1].getP(1);
double dist=Vector2D.dist(new Vector2D(startP), new Vector2D(endP));
this.closed=false;
if(dist<Curve2D.eps) closed=true;
for(int i=0;i<segments.length;i++) {
Shape shape=segments[i].getShape();
this.generalPath.append(shape,true);
}
if(this.closed) this.generalPath.closePath();
|
|
setData
|
public void setData(Segment2D[] segments)
Performs the same processing as the constructor.
|
getType2DE
(abstract)
|
public abstract int getType2DE()
Return the type of this parametric curve.
The types are RECTANGLE,
ROUND_RECTANGLE, ELLIPSE and so on.
|
|
getShape
|
public Shape getShape()
Return the generalPath field.
 =>
Creating and extracting java.awt.Shape =>
Creating and extracting java.awt.Shape
|
| isClosed |
public boolean isClosed()
Rturns the closed field. |
|
getNumOfSegments
|
public int getNumOfSegments()
Returns the number of the curve segments (segments field).
|
|
getSegment2Ds
|
public Segment2D[] getSegment2Ds()
Return the segments.
|
|
getSegment2D
|
public Segment2D getSegment2D(int Index)
Return the curve segment specified by the index.
|
|
getP
|
public Point2D getP(double t)
Parameter:
t - The parameter of the curve segment.
0≤t≤nseg, nseg: the returned value of the getNumOfSegments.
Returns:
The position (x,y) of the parametric curve at the t.
|
|
getTangent
|
public Vector2D getTangent(double t)
Parameter:
t - The parameter of the curve segment.
0≤t≤nseg, nseg: the returned value of the getNumOfSegments.
Returns:
The derivative (tangent vector) of the parametric curve at the t.
|
| getTangentDerivative |
public Vector2D getTangentDerivative(double t)
Parameter:
t - The parameter of the curve segment.
0≤t≤nseg, nseg: the returned value of the getNumOfSegments.
Returns:
The second derivative vector of the parametric curve at the t.
|
| getEndPoints |
public Point2D[] getEndPoints()
Returns the endpoints.
|
| getCharacteristicPoints |
public CurvePT[] getCharacteristicPoints()
Returns the characteristic points. The characteristic points are endpoints
of a line/curve segment, and north, south, east and west points of an ellipse/circle.
 =>
ConnectionLS Figure 1 =>
ConnectionLS Figure 1
|
|
getCurveLength
|
public double getCurveLength(double t1, double t2)
Parameters:
t1 - The start parameter of the interval.
t2 - The end parameter of the interval.
0≤t1, t2≤nseg, nseg: the returned value of the getNumOfSegments.
Returns:
Returns the curve length of the interval (t1≤t≤t2).
|
|
getBoundingBox
|
public Rectangle2D getBoundingBox()
Returns the bounding box enclosing the parametric curve.
|
|
getBoundingBox
|
public Rectangle2D getBoundingBox(double t1, double t2)
Parameters:
t1 - The start parameter of the interval.
t2 - The end parameter of the interval.
0≤t1, t2≤nseg, nseg: the returned value of the
getNumOfSegments.
Returns:
Returns the bounding box enclosing the curve interval (t1≤t≤t2) of the parametric curve.
|
|
getSerializableCurve2D
|
public SerializableCurve2D getSerializableCurve2D()
Returns:
The SerializableCurve2D object
which is used for writing this object to the file.
|
| setSerializableCurve2D |
public void setSerializableCurve2D(SerializableCurve2D sdata)
Parameters:
sdata - The SerializableCurve2D object
which is used for writing this object to the file.
Processing:
Sets the contents of the sdata to this object.
|
convertToGeneral
Curve2DE
|
public GeneralCurve2DE convertToGeneralCurve2DE()
Converts this object to the GeneralCurve2DE object.
This method is used for rotating Rectangle2DE, RoundRectangle2D etc.
|
| reverse |
public void reverse()
Reverses the direction of parametric curve by using the
Segment2D.reverseSegment.
|
| transform |
public void transform(Matrix2D M)
Parameters:
M - The transforming matrix.
Processing:
Transforms the parametric curve by using the
Segment2D.transformSegment method.
|
clone
(abstract)
|
public abstract Object clone()
Returns the clone of this object.
|
toString
(abstract)
|
public abstract String toString()
Returns the string representing this object.
|
5. Class Rectangle2DE
return=>page top
public class Rectangle2DE extends Curve2D
| Method |
Description |
| Constructor |
Rectangle2DE(Segment2D[] segments)
Calls the Curve2D constructor.
|
|
Constructor
|
public Rectangle2DE(double x, double y, double width, double height)
Parameters:
The same as the java.awt.geom.Rectangle2D.Double.
Processing:
Creates a new Rectangle2DE object by connecting the four
Segment2D objects of LINE.
|
|
getType2DE
|
public int getType2DE()
Returns the constant of Curve2D.RECTANGLE.
|
|
getX
|
public double getX()
Same as the getX method of the java.awt.geom.Rectangle2D.
Returns the x-coordinate of the upper-left corner point of the rectangle.
|
|
getY
|
public double getY()
Same as the getY method of the java.awt.geom.Rectangle2D.
Returns the y-coordinate of the upper-left corner point of the rectangle.
|
|
getWidth
|
public double getWidth()
Same as the getWidth method of the java.awt.geom.Rectangle2D.
Returns the width of the rectangle.
|
|
getHeight
|
public double getHeight()
Same as the getHeight method of the java.awt.geom.Rectangle2D.
Returns the height of the rectangle.
|
|
clone
|
public Object clone()
Returns the clone of this object.
|
|
toString
|
public String toString()
Returns the string representing this object.
|
6. RoundRectangle2DE
return=>page top
public class RoundRectangle2DE extends Curve2D
| Method |
Description |
| Constructor |
RoundRectangle2DE(Segment2D[] segments)
Calls the Curve2D constructor.
|
|
Constructor
|
public RoundRectangle2DE(double x, double y, double width, double height,
double arcw, double arch)
Parameters:
The same as the java.awt.geom.RoundRectangle2D.Double.
Processing:
Creates a new RoundRectangle2DE object by connecting the eight Segment2D
objects of LINE and ARC.
|
| setData |
public void setData(double x, double y, double width, double height, double
arcw, double arch)
Performs the same operation of the above constructor. |
|
getType2DE
|
public int getType2DE()
Returns the constant of Curve2D.ROUND_RECTANGLE.
|
|
getX
|
public double getX()
Same as the getX method of the java.awt.geom.RoundRectangle2D.
Returns the x-coordinate of the upper-left corner point of the round rectangle.
|
|
getY
|
public double getY()
Same as the getY method of the java.awt.geom.RoundRectangle2D.
Returns the y-coordinate of the upper-left corner point of the round rectangle.
|
|
getWidth
|
public double getWidth()
Same as the getWidth method of the java.awt.geom.RoundRectangle2D.
Returns the width of the round rectangle.
|
|
getHeight
|
public double getHeight()
Same as the getHeight method of the java.awt.geom.RoundRectangle2D.
Returns the height of the round rectangle.
|
|
getArcWidth
|
public double getArcWidth()
Returns the width of the arc that rounds off the corners.
|
getArcHeight
|
public double getArcHeight()
Returns the height of the arc that rounds off the corners.
|
clone
|
public Object clone()
Returns the clone of this object.
|
|
toString
|
public String toString()
Returns the string representing this object.
|
7. Ellipse2DE
return=>page top
public class Ellipse2DE extends Curve2D
| Method |
Description |
| Constructor |
Ellipse2DE(Segment2D[] segments)
Calls the Curve2D constructor.
|
|
Constructor
|
public Ellipse2DE(double x, double y, double width, double height)
Parameters:
The same as the java.awt.geom.Ellipse2D.Double.
Processing:
Creates a new Ellipse2DE object by the Segment2D
object of ARC.
|
|
getType2DE
|
public int getType2DE()
Returns the constant of Curve2D.ELLIPSE.
|
|
getX
|
public double getX()
Same as the getX method of the java.awt.geom.Ellipse2D.
Returns the x-coordinate of the upper-left corner point of the covering rectangle.
|
|
getY
|
public double getY()
Same as the getY method of the java.awt.geom.Ellipse2D.
Returns the y-coordinate of the upper-left corner point of the covering rectangle.
|
|
getWidth
|
public double getWidth()
Same as the getWidth method of the java.awt.geom.Ellipse2D.
Returns the width of the covering rectangle.
|
|
getHeight
|
public double getHeight()
Same as the getHeight method of the java.awt.geom.Ellipse2D.
Returns the height of the covering rectangle.
|
|
clone
|
public Object clone()
Returns the clone of this object.
|
|
toString
|
public String toString()
Returns the string representing this object.
|
8. Line2DE
return=>page top
public class Line2DE extends Curve2D
| Method |
Description |
| Constructor |
Line2DE(Segment2D[] segments)
Calls the Curve2D constructor.
|
|
Constructor
|
Line2DE(Point2D p1, Point2D p2)
Parameters:
The same as the java.awt.geom.Line2D.Double.
Processing:
Creates a new Line2DE object by the Segment2D
object of LINE.
|
|
getType2DE
|
public int getType2DE()
Returns the constant of Curve2D.LINE.
|
|
setData
|
public void setData(Point2D p1, Point2D p2)
Performs the same operation of the above constructor.
|
|
getP1
|
public Point2D getP1()
Returns the start point.
|
|
getP2
|
public Point2D getP2()
Returns the end point.
|
|
getX1
|
public double getX1()
Returns the x coordinate of the start point.
|
|
getY1
|
public double getY1()
Returns the y coordinate of the start point.
|
|
getX2
|
public double getX2()
Returns the x coordinate of the end point.
|
|
getY2
|
public double getY2()
Returns the y coordinate of the end point.
|
| getTrimmedCurve2DE |
public Line2DE getTrimmedCurve2DE(double t1, double t2)
Parameters:
t1 - The start parameter of the trimmed curve.
t2 - The end parameter of the trimmed curve.
0≤t1, t2≤1
Returns:
The trimmed Line2DE object.
|
| getTrimmedLine |
public Line2DE getTrimmedLine(double cut1, double cut2)
Parameters:
cut1 - The cutting length (pixels) at the start point.
cut2 - The cutting length (pixels) at the end point.
Returns:
The trimmed Line2DE object.
Processing:
This method uses the getTrimmedCurve2DE.
|
|
clone
|
public Object clone()
Returns the clone of this object.
|
|
toString
|
public String toString()
Returns the string representing this object.
|
9. Polyline2DE
return=>page top
public class Polyline2DE extends Curve2D
| Method |
Description |
| Constructor |
Polyline2DE(Segment2D[] segments)
Calls the Curve2D constructor.
|
|
Constructor
|
public Polyline2DE(Point2D[] points)
Creates a new Polyline2DE object by the junction points.
Whether this Polyline2DE is closed or not is judged by the
Curve2D.ClosedTolerance.
|
|
Constructor
|
public Polyline2DE(Point2D[] points, boolean closed)
Creates a new Polyline2DE object by the junction points.
Whether this Polyline2DE is closed or not is specified explicitly by the parameter.
|
|
setData
|
public void setData(Point2D[] points)
Performs the same operation of the above constructor.
|
|
getType2DE
|
public int getType2DE()
Returns the constant of Curve2D.POLYLINE.
|
|
getPoints
|
public Point2D[] getPoints()
Returns the junction points.
|
|
getPoint
|
public Point2D getPoint(int index)
Return the junction point specified by index.
|
|
getTrimmedCurve2DE
|
public Polyline2DE getTrimmedCurve2DE(double t1, double t2)
Parameters:
t1 - The start parameter of the trimmed curve.
t2 - The end parameter of the trimmed curve.
0≤t1, t2≤nseg. nseg: the returned value of the getNumOfSegments.
Returns:
The trimmed Polyline2DE object.
|
| getTrimmedPolyline |
public Polyline2DE getTrimmedPolyline(double cut1, double cut2)
Parameters:
cut1 - The cutting length (pixels) at the start point.
cut2 - The cutting length (pixels) at the end point.
Returns:
The trimmed Polyline2DE object.
Processing:
This method uses the getTrimmedCurve2DE.
|
|
clone
|
public Object clone()
Returns the clone of this object.
|
|
toString
|
public String toString()
Returns the string representing this object.
|
10. CubicCurve2DE
return=>page top
public class CubicCurve2DE extends Curve2D
| Method |
Description |
| Constructor |
CubicCurve2DE(Segment2D[] segments)
Calls the Curve2D constructor.
|
|
Constructor
|
public CubicCurve2DE(Point2D[] Q)
Creates a new CubicCurve2DE object by the control points.
The number of the control points must be 3*n+1. Here "n" is the
number of curve segments (Segment2D objects).
|
|
setData
|
public void setData(Point2D[] points)
Performs the same operation of the above constructor.
|
|
getType2DE
|
public int getType2DE()
Returns the constant of Curve2D.CUBIC_CURVE.
|
|
getPoints
|
public Point2D[] getPoints()
Returns the segment junction points. The segment junction point means the junction point of the
curve segments.
|
|
getCtrlPoints
|
public Point2D[] getCtrlPoints()
Returns the control points.
|
|
getFergusonCurve2D
|
public FergusonCurve2D getFergusonCurve2D()
Converts this multiple cubic curves to the Feguson curve and returns the Feguson
curve (FergusonCurve2DE).
|
|
getTout
|
public Vector2D getTout(int index)
Parameter:
index - The index of the segment junction point.
Returns:
The the tangent line (OUT) at the plus side of the specified node point.
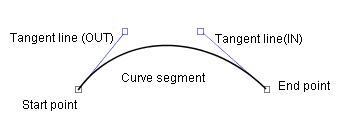
|
|
getTin
|
public Vector2D getTin(int index)
Paremeter:
index - The index of the segment junction point.
Returns:
The tangent line (IN) at the minus side of the specified node point.
|
|
getTrimmedCurve2DE
|
public CubicCurve2DE getTrimmedCurve2DE(double t1, double t2)
t1 - The start parameter of the trimmed curve.
t2 - The end parameter of the trimmed curve.
0≤t1, t2≤nseg. nseg: the returned value of the getNumOfSegments.
Returns:
The trimmed CubicCurve2DE object.
|
|
clone
|
public Object clone()
Returns the clone of this object.
|
|
toString
|
public String toString()
Returns the string representing this object.
|
11. GeneralCurve2DE
return=>page top
public class GeneralCurve2DE extends Curve2D<
This class represents a parametric curve which consists of arbitrary number of subpaths.
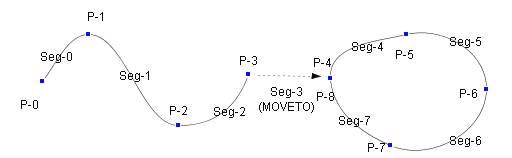
Figure 11.1 Global numbering of the segments and junction points
Segment number: Seg-0, Seg-1,..., Segment point (Junction point) number:
P-0, P-1,....
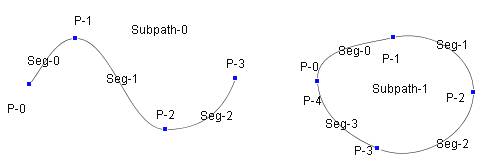
Figure 11.2 Local numbering of the segments and junction points
The segments and the junction points are numbered from 0 for each
sub path. |
(a) Prints out the 0-7 segments
segment[0]=CUBIC, P1=640.04,371.28, P2=685.90,324.95, CtrlP1=654.01,353.07,CtrlP2=665.80,324.95
segment[1]=CUBIC, P1=685.90,324.95, P2=775.45,415.98, CtrlP1=722.90,324.95, CtrlP2=738.46,415.93
segment[2]=CUBIC, P1=775.45,415.98, P2=846.18,364.98, CtrlP1=801.94,416.01, CtrlP2=831.32,406.89
segment[3]=MoveTo
segment[4]=CUBIC, P1=928.82,371.58, P2=1,004.96,328.01, CtrlP1=926.56,337.66, CtrlP2=975.82,334.84
segment[5]=CUBIC, P1=1,004.96,328.01, P2=1,085.27,382.36, CtrlP1=1,041.93,319.35, CtrlP2=1,086.01,344.76
segment[6]=CUBIC, P1=1,085.27,382.36, P2=989.42,438.44, CtrlP1=1,084.42,425.39, CtrlP2=1,029.39,455.40
segment[7]=CUBIC, P1=989.42,438.44, P2=928.82,371.58, CtrlP1=960.27,426.07, CtrlP2=931.06,405.02
(2) Prints out 0-7 segments in subpath-form
- sub path=0, close=false, numseg=3, startSegment=0, endSegment=2 [ start t-param=0, end t-param=3 ]
segment[0]=CUBIC, P1=640.04,371.28, P2=685.90,324.95, CtrlP1=654.01,353.07, CtrlP2=665.80,324.95
segment[1]=CUBIC, P1=685.90,324.95, P2=775.45,415.98, CtrlP1=722.90,324.95, CtrlP2=738.46,415.93
segment[2]=CUBIC, P1=775.45,415.98, P2=846.18,364.98, CtrlP1=801.94,416.01, CtrlP2=831.32,406.89
- sub path=1, close=true, numseg=4, startSegment=4, endSegment=7 [ start t-param=4, end t-param=8 ]
segment[0]=CUBIC, P1=928.82,371.58, P2=1,004.96,328.01, CtrlP1=926.56,337.66, CtrlP2=975.82,334.84
segment[1]=CUBIC, P1=1,004.96,328.01, P2=1,085.27,382.36, CtrlP1=1,041.93,319.35, CtrlP2=1,086.01,344.76
segment[2]=CUBIC, P1=1,085.27,382.36, P2=989.42,438.44, CtrlP1=1,084.42,425.39, CtrlP2=1,029.39,455.40
segment[3]=CUBIC, P1=989.42,438.44, P2=928.82,371.58, CtrlP1=960.27,426.07, CtrlP2=931.06,405.02
|
| Method |
Description |
| Constructor |
GeneralCurve2DE(Segment2D[] segments)
Calls the following setData method.
|
| setData |
public void setData(Segment2D[] segments)
Sets the segments (Segment2D objects) to this object.
For the Figure 11.1 example, sets the 8 segments
inclideing one MOVETO segment.
|
|
getType2DE
|
public int getType2DE()
Returns the constant of Curve2D.GENERAL_CURVE.
|
| getNumOfSubPaths |
public int getNumOfSubPaths()
Returns the number of the subpaths of this object. Returns 2 for the Figure 11.1 example.
|
| getNumOfLocalSegments |
public int[] getNumOfLocalSegments()
Returns each number of the segments which
configures a subpaths.
For the Figure 11.1 example, returns int[0]=3, int[0]=4, which means the
first path consists of 3 segments and the second path consists of 4 segments.
|
| getSubPathIndex |
public int getSubPathIndex(int segmentPtIndex)
Return the subpath number for the argument which specifies a segment number
or segment joint number.
For the Figure 11.1 example, returns 0 as the subPath index for segmentPtIndex=0
- 3, and returns 1 as the subPath index for segmentPtIndex=4 - 8.
|
| getLocalSegmentIndex |
private int getLocalSegmentIndex(int segmentIndex)
Returns the local segment number of a sub path for the specified argument which is the global segment number.
The sub path number can be givven by getSubPathIndex method.
For the Figure 11.1 example, returns as follows.
⋅ segmentIndex=0 - 2 => localSegmentIndex=0 - 2,
⋅ segmentIndex=4 - 7 => localSegmentIndex=0 - 3,
⋅ segmentIndex=3 => localSegmentIndex=-1(MOVETO segment, ineffective)
|
| getLocalSegmentPtIndex |
public int getLocalSegmentPtIndex(int segmentPtIndex)
Returns the local segment junction point number of a sub path for the specified
argument which is the global segment junction point number. The sub path number
can be givven by getSubPathIndex method.
For the Figure 11.1 example, returns as follows.
⋅ segmentPtIndex=0 - 3=>localSegmentPtIndex=0 - 3.
⋅ segmentPtIndex=4 - 8=>localSegmentPtIndex=0 - 4.
|
| getGlobalSegmentIndex |
private int getGlobalSegmentIndex(int subPathIndex, int localSegmentIndex)
Return the global segment number for the specified arguments which are
sub path number and the local segment number.
For the Figure 11.1 example, returns as follows.
⋅ subPathIndex=0, localSegmentIndex=0 - 2 => globalSegmentIndex=0 - 2.
⋅ subPathIndex=1, localSegmentIndex=0 - 3 => globalSegmentIndex=4 -
7.
⋅ return -1 (ineffective) except the aboves.
|
| getGlobalSegmentPtIndex |
public int getGlobalSegmentPtIndex(int subPathIndex, int localSegmentPtIndex)
Return the global segment junction point number for the specified arguments which are sub path number and the local segment junction point number.
For the Figure 11.1 example, returns as follows.
⋅ subPathIndex=0, localSegmentPtIndex=0 - 3 => globalSegmentPtIndex=0
- 3.
⋅ subPathIndex=1, localSegmentPtIndex=0 - 4 => globalSegmentPtIndex=4
- 8.
⋅ return -1 (ineffective) except the aboves.
|
| getSubPathSegments |
private Segment2D[] getSubPathSegments(int subPathIndex)
Returns the segments which belong to the sub path specified by argument.
For the Figure 11.1 example, returns as follows.
⋅ subPathInde=0 => returns 0 - 2 segments.
⋅ subPathInde=1 => returns 4 -7 segments.
|
| getSubPath |
private GeneralCurve2DE getSubPath(int index)
Returns the sub path curve as a GeneralCurve2DE object for the specified
argument which is sub path number.
For the Figure 11.1 example, returns as follows.
⋅ subPathInde=0 => GeneralCurve2DE object which consists of 0 -
2 segments.
⋅ subPathInde=1 => GeneralCurve2DE object which consists of 4 - 7 segments.
|
| getSubPaths |
public GeneralCurve2DE[] getSubPaths()
Returns the array the sub paths which are represented as GeneralCurve2DE objects.
|
| setSubPaths |
public void setSubPaths(Curve2D[] curves)
Specifies the plural sub paths as the arguments
and sets them to this object.
⋅ Checks the connections between the specified sub paths by the
PathConnect class, and connects them if possible.
|
| isClosed |
public boolean isClosed()
Return true, if the sub path of this object is only one
and it is closed. Returns false for the othe case.
To confirm closed or not closed for each subpath, use getPaths method and
inquire by isClosed method of each sub path object.
|
|
getTrimmedCurve2DE
|
public CubicCurve2DE getTrimmedCurve2DE(double t1, double t2)
t1 - The start parameter of the trimmed curve.
t2 - The end parameter of the trimmed curve.
0≤t1, t2≤nseg. nseg: the returned value of the getNumOfSegments.
Returns:
The trimmed GeneralCurve2DE object.
|
| getSimpleCurve2Ds |
public Curve2D[] getSimpleCurve2Ds()
|
| getSimpleCurve2D |
public Curve2D getSimpleCurve2D()
Returns:
The Curve2DE object of simpler form.
Processing:
If this GeneralCurve2DE can be converted to Line2DE,Polyline2DE or CubicCurve2DE,
then converts the GeneralCurve2DE to simpler form and returns it.
|
|
clone
|
public Object clone()
Returns the clone of this object.
|
|
toString
|
public String toString()
Returns the string representing this object.
|
12. FergusonCurve2D
return=>page top
public class FergusonCurve2D
This class is not a extended class of the Curve2D and it represents the Ferguson curve.
The Ferguson curve is convenient for handling the tangent vectors of the curve segment because
the tangent vectors are expressed explicitly.
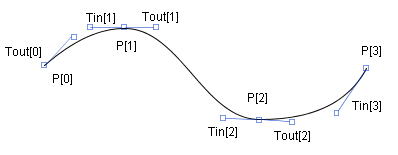
Figure 12.1 Ferguson curve
 => The definition of Tin, Tout => The definition of Tin, Tout
| Field |
Description |
|
P
|
Point2D[] P
The array of the segment junction points.
|
| Tin |
Vector2D[] Tin
The array of the tangent vectors at the segment junction points which interpolate
the next curve segments.
 =>
Ferguson curve segment on this page =>
Ferguson curve segment on this page
|
| Tout |
Vector2D[] Tout
The array of the tangent vectors at the segment junction points which interpolate the
previous curve segments.
 =>
Ferguson curve segment on this page =>
Ferguson curve segment on this page
|
| closed |
boolean closed
True if the curve is closed.
|
| pai |
static double pai=Math.PI
The circle ratio.
|
| eps |
static double eps=1e-12
The small number. |
| TIN, TOUT |
public static final int TIN=0, TOUT=1 |
| Method |
Description |
|
Constructor
|
public FergusonCurve2D()
Creates a new object that has no curve data.
|
|
Constructor
|
public FergusonCurve2D(Point2D[] P, Vector2D[] Tin, Vector2D[] Tout)
Parameters:
P - The array of the segment junction points.
Tin - The array of the tangent vectors at the segment junction points which interpolate the next curve segments
Tout - The array of the tangent vectors at the segment junction points which interpolate
the previous curve segments.
Processing:
Sets the parameters to corresponding fields.
If P[0}=P[np-1], then sets true to the closed field.
np: the number of the segment junction points.
|
|
isClosed
|
public boolean isClosed()
Return the closed field.
|
|
getNumOfSegments
|
public int getNumOfCSegments()
Returns the number of the curve segments.
|
|
getCubicCurve2DE
|
public CubicCurve2DE getCubicCurve2DE()
Returns the CubicCurve2DE object which is converted from this object.
|
|
getCubicCurve2D
|
public CubicCurve2D getCubicCurve2D(int index)
Returns the java.awt.geom.CubicCurve2D object which is converted from the
curve segment of this object specified by the index.
|
|
getCtrlPoints
|
public Point2D[] getCtrlPoints()
Converts this FergusonCurve2D object to the CubicCurve2DE
object and returns the control points of the CubicCurve2DE.
The number of the control points is (3×(np-1)+1).
np: the number of the segment junction points.
|
|
getP
|
public Point2D getP(int index)
Returns the segment junction point specified by the index.
|
|
setP
|
public void setP(Point2D P, int index)
Sets the point P to the P at the position specified by the index.
|
|
getTin
|
public Vector2D getTin(int index)
Returns the Tin (tangent vector) specified by the index.
|
|
setTin
|
public void setTin(Vector2D Tin, int index)
Sets the tangent vector Tin to the Tin
at the position specified by the index..
|
|
getTout
|
public Vector2D getTout(int index)
Returns the Tout (tangent vector) specified by the index.
|
|
setTout
|
public void setTout(Vector2D Tout, int index)
Sets the tangent vector Tout to the Tout
at the position specified by the index.
|
|
getP
|
public Point2D getP(double t)
Returns the point on the Fergusn curve specified by t.
|
|
getTangent
|
public Vector2D getTangent(double t)
Returns the tangent vector on the Fergusn curve specified by t.
|
|
movePoint
|
public void movePoint(int index, Point2D newPoint)
Paremeters:
index - The index of the segment junction point to be moved.
newPoint - the new segment junction point.
Processing:
Replace the segment junction point (P[index]) by the newPoint.
The directions of the Tout[index-1],
Tin[index], Tout[index] and
Tin[index+1] are not changed,
however the lengths of those vectors are optimized
by the getOptimizedTangents method.
|
|
moveTangent
|
public void moveTangent(int index, Vector2D newTangent)
Paremeters:
index - The index of the segment junction point.
newTangent - The new tangent vector.
The direction of the newTangent will be referred (the length isn't referred).
Processing:
Replaces the direction of the Tin[index],
Tout[index] by the newTangent.
The lengths of the Tout[index-1],
Tin[index], Tout[index]
and Tin[index+1] are optimized by the
getOptimizedTangents method.
|
|
addPoint
|
public void addPoint(double t)
Parameters:
t - The curve parameter of the point to be added.
Processing:
Adds the segment junction point at the parameter of t.
Let's define as it= (int)t, then the new segment junction point is indicated by the index of
(it+1).
The point and the Tin, Tout at t can be calculated by the getP and the getTangent, so by adding these data to P[it+1], Tin[it+1] and Tout[it+1], the new Ferguson curve will be created.
However the length of the Tout[it],
Tin[it+1], Tout[it+1]
and Tin[it+2] must be changed
so that any point on the new curve lies on the original curve.
The formulas of the new lengths are the follows.
⋅ The lengths of Tout[it], Tin[it+1]:Provided by the formula of (t-it)*(the original length).
⋅ The lengths of Tout[it+1], Tin[it+2]:Provided by the formula of (i+1-t)*(the original length).
|
|
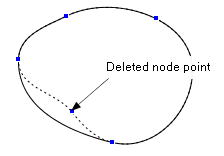
deletePoint
|
public void deletePoint(int index)
Parameters:
index - The index of the segment junction point to be delete.
Processing:
Deletes the P[index], Tin[index] and Tout[index] and creates a new curve.
If the original curve is closed, then the new curve must be closed.
|
|
toString
|
public String toString()
Return the string representing this object.
|
createNaturalSpline
(static)
|
public static FergusonCurve2D createNaturalSpline(Point2D[] nodePTs)
Paremeters:
nodePTs - The segment junction points of the spline
Returns:
The C2 class spline curve of Furguson curve format.
Processing:
Creates the C2 class spline curve which passes the given segment junction points (nodePTs).
⋅ If the start point and the end point of the given points doesn't occupy
the same location, then performs the following.
Calls the getUnitTangentOfOpenCurve method
to determine the tangent directions at the given points for a open (not closed) spline.
⋅ If the start point and the end point of the given points occupies the
same location, then performs the following.
Calls the getUnitTangentOfOpenCurve method
to determine the tangent directions at the given points for a closed spline.
The length of the tangent vectors are determined by the the
Curve2DUtil.createCircularArcs method.
|
getUnitTangentOf
OpenCurve
(static)
|
public static Vector2D[] getUnitTangentOfOpenCurve(Point2D[] nodePTs)
Parameters:
nodePTs - The segment junction points of the spline.
Returns:
The unit tangent vectors at the nodePTs.
Processing:
Solves the linear equation by the Matrix.GaussianElimination method.
The linear equation is created by the condition of the C2 class continuity of the spline
at each segment junction point.
The tangent vectors at the start node and the end node are calculated by the the
Curve2DUtil.createCircularArcs method .
|
getUnitTangentOf
ClosedCurve
(static)
|
public static Vector2D[] getUnitTangentOfClosedCurve(Point2D[] nodePTs)
Parameters:
nodePTs - The segment junction points of the spline.
Returns:
The unit tangent vectors at the nodePTs.
Processing:
Solves the linear equation by the Matrix.GaussianElimination method.
The linear equation is created by the condition of the C2 class continuity
of the spline at each segment junction point.
|
getOptimizedTangents
(static)
|
public static Vector2D[] getOptimizedTangents(Point2D P0, Point2D P1, Vector2D
Tout, Vector2D Tin)
Parameters:
P0 - The first segment junction point.
P1 - The second segment junction point.
Tout - The first tangent vector.
Tin - The second tangent vector.
Returns:
The new Tout, Tin vectors.
This method changes the lengths of the Tout and Tin without changing their directions.
Processing:
The notations in the figure below are as follows.
⋅ The line of P0,Q0: The normal line of the Tout.
⋅ The line of P1,Q1: The normal line of the Tin.
⋅ P01: The middle point of P0, P1.
⋅ The line of P01, Q1: The normal line of the line of P0, P1.
The optimized vector length |Tout|, |Tin| are calculated as follows.
|Tout|=4.0*r0*(1-cos(teta0))/sin(teta0)
|Tin| =4.0*r1*(1-cos(teta1))/sin(teta1)
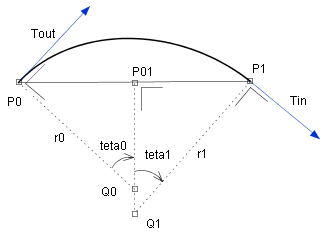
 :
If the Tout and Tin are parallel, then the lengths of Tout and Tin are the same as
the line length of P0, P1. :
If the Tout and Tin are parallel, then the lengths of Tout and Tin are the same as
the line length of P0, P1.
|
|
![]()
![]()
![]()
![]()
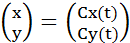 (1)
(1) =>
Figure 1.1 (a)
=>
Figure 1.1 (a)
 :
Returning the transformed Arc2D
:
Returning the transformed Arc2D => The definition of Tin, Tout
=> The definition of Tin, Tout